Lecture 12: Feature importances and model transparency

Lecture 12: Feature importances and model transparency#

UBC 2023-24

Instructor: Varada Kolhatkar

Imports, announcements, LOs#

Imports#

import os
import string
import sys
from collections import deque

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

sys.path.append(os.path.join(os.path.abspath("."), "code"))
import seaborn as sns
from plotting_functions import *
from sklearn import datasets
from sklearn.compose import ColumnTransformer, make_column_transformer
from sklearn.dummy import DummyClassifier, DummyRegressor
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LogisticRegression, Ridge
from sklearn.model_selection import (
    GridSearchCV,
    RandomizedSearchCV,
    cross_val_score,
    cross_validate,
    train_test_split,
)
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.preprocessing import OneHotEncoder, OrdinalEncoder, StandardScaler
from sklearn.svm import SVC, SVR
from sklearn.tree import DecisionTreeClassifier
from utils import *

%matplotlib inline

Learning outcomes#

From this lecture, students are expected to be able to:

Interpret the coefficients of linear regression for ordinal, one-hot encoded categorical, and scaled numeric features.
Explain why interpretability is important in ML.
Use feature_importances_ attribute of sklearn models and interpret its output.
Apply SHAP to assess feature importances and interpret model predictions.
Explain force plot, summary plot, and dependence plot produced with shapely values.

import warnings

warnings.simplefilter(action="ignore", category=FutureWarning)

Announcement#

Midterm is next week.
- Bring your laptop. Make sure that it’s fully charged.
- Bring your UBC ID Card.
HW5 is available.
My OH on Thursday has been cancelled. I’ll hold OH on Tuesday instead.

I’m using seaborn in this lecture for easy heatmap plotting, which is not in the course environment. You can install it as follows.

> conda activate cpsc330
> conda install -c anaconda seaborn

import warnings

warnings.simplefilter(action="ignore", category=FutureWarning)

Data#

In the first part of this lecture, we’ll be using Kaggle House Prices dataset, the dataset we used in lecture 10. As usual, to run this notebook you’ll need to download the data. Unzip the data into a subdirectory called data. For this dataset, train and test have already been separated. We’ll be working with the train portion in this lecture.

df = pd.read_csv("data/housing-kaggle/train.csv")
train_df, test_df = train_test_split(df, test_size=0.10, random_state=123)
train_df.head()

	Id	MSSubClass	MSZoning	LotFrontage	LotArea	Street	Alley	LotShape	LandContour	Utilities	...	PoolQC	Fence	MiscFeature	MiscVal	MoSold	YrSold	SaleType	SaleCondition	SalePrice
302	303	20	RL	118.0	13704	Pave	NaN	IR1	Lvl	AllPub	...	NaN	NaN	NaN	0	1	2006	WD	Normal	205000
767	768	50	RL	75.0	12508	Pave	NaN	IR1	Lvl	AllPub	...	NaN	NaN	Shed	1300	7	2008	WD	Normal	160000
429	430	20	RL	130.0	11457	Pave	NaN	IR1	Lvl	AllPub	...	NaN	NaN	NaN	0	3	2009	WD	Normal	175000
1139	1140	30	RL	98.0	8731	Pave	NaN	IR1	Lvl	AllPub	...	NaN	NaN	NaN	0	5	2007	WD	Normal	144000
558	559	60	RL	57.0	21872	Pave	NaN	IR2	HLS	AllPub	...	NaN	NaN	NaN	0	8	2008	WD	Normal	175000

5 rows × 81 columns

The prediction task is predicting SalePrice given features related to properties.
Note that the target is numeric, not categorical.

train_df.shape

(1314, 81)

Let’s separate `X` and `y`#

X_train = train_df.drop(columns=["SalePrice"])
y_train = train_df["SalePrice"]

X_test = test_df.drop(columns=["SalePrice"])
y_test = test_df["SalePrice"]

Let’s identify feature types#

drop_features = ["Id"]
numeric_features = [
    "BedroomAbvGr",
    "KitchenAbvGr",
    "LotFrontage",
    "LotArea",
    "OverallQual",
    "OverallCond",
    "YearBuilt",
    "YearRemodAdd",
    "MasVnrArea",
    "BsmtFinSF1",
    "BsmtFinSF2",
    "BsmtUnfSF",
    "TotalBsmtSF",
    "1stFlrSF",
    "2ndFlrSF",
    "LowQualFinSF",
    "GrLivArea",
    "BsmtFullBath",
    "BsmtHalfBath",
    "FullBath",
    "HalfBath",
    "TotRmsAbvGrd",
    "Fireplaces",
    "GarageYrBlt",
    "GarageCars",
    "GarageArea",
    "WoodDeckSF",
    "OpenPorchSF",
    "EnclosedPorch",
    "3SsnPorch",
    "ScreenPorch",
    "PoolArea",
    "MiscVal",
    "YrSold",
]

ordinal_features_reg = [
    "ExterQual",
    "ExterCond",
    "BsmtQual",
    "BsmtCond",
    "HeatingQC",
    "KitchenQual",
    "FireplaceQu",
    "GarageQual",
    "GarageCond",
    "PoolQC",
]
ordering = [
    "Po",
    "Fa",
    "TA",
    "Gd",
    "Ex",
]  # if N/A it will just impute something, per below
ordering_ordinal_reg = [ordering] * len(ordinal_features_reg)
ordering_ordinal_reg

[['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
 ['Po', 'Fa', 'TA', 'Gd', 'Ex']]

ordinal_features_oth = [
    "BsmtExposure",
    "BsmtFinType1",
    "BsmtFinType2",
    "Functional",
    "Fence",
]
ordering_ordinal_oth = [
    ["NA", "No", "Mn", "Av", "Gd"],
    ["NA", "Unf", "LwQ", "Rec", "BLQ", "ALQ", "GLQ"],
    ["NA", "Unf", "LwQ", "Rec", "BLQ", "ALQ", "GLQ"],
    ["Sal", "Sev", "Maj2", "Maj1", "Mod", "Min2", "Min1", "Typ"],
    ["NA", "MnWw", "GdWo", "MnPrv", "GdPrv"],
]

categorical_features = list(
    set(X_train.columns)
    - set(numeric_features)
    - set(ordinal_features_reg)
    - set(ordinal_features_oth)
    - set(drop_features)
)
categorical_features

['Condition1',
 'MSSubClass',
 'LandSlope',
 'SaleCondition',
 'CentralAir',
 'MoSold',
 'Electrical',
 'GarageFinish',
 'Neighborhood',
 'GarageType',
 'Exterior1st',
 'MiscFeature',
 'Utilities',
 'Condition2',
 'MSZoning',
 'BldgType',
 'Heating',
 'Street',
 'LotConfig',
 'Exterior2nd',
 'MasVnrType',
 'HouseStyle',
 'Alley',
 'SaleType',
 'LandContour',
 'LotShape',
 'RoofMatl',
 'PavedDrive',
 'Foundation',
 'RoofStyle']

from sklearn.compose import ColumnTransformer, make_column_transformer

numeric_transformer = make_pipeline(SimpleImputer(strategy="median"), StandardScaler())
ordinal_transformer_reg = make_pipeline(
    SimpleImputer(strategy="most_frequent"),
    OrdinalEncoder(categories=ordering_ordinal_reg),
)

ordinal_transformer_oth = make_pipeline(
    SimpleImputer(strategy="most_frequent"),
    OrdinalEncoder(categories=ordering_ordinal_oth),
)

categorical_transformer = make_pipeline(
    SimpleImputer(strategy="constant", fill_value="missing"),
    OneHotEncoder(handle_unknown="ignore", sparse=False),
)

preprocessor = make_column_transformer(
    ("drop", drop_features),
    (numeric_transformer, numeric_features),
    (ordinal_transformer_reg, ordinal_features_reg),
    (ordinal_transformer_oth, ordinal_features_oth),
    (categorical_transformer, categorical_features),
)

preprocessor.fit(X_train)
preprocessor.named_transformers_

{'drop': 'drop',
 'pipeline-1': Pipeline(steps=[('simpleimputer', SimpleImputer(strategy='median')),
                 ('standardscaler', StandardScaler())]),
 'pipeline-2': Pipeline(steps=[('simpleimputer', SimpleImputer(strategy='most_frequent')),
                 ('ordinalencoder',
                  OrdinalEncoder(categories=[['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex'],
                                             ['Po', 'Fa', 'TA', 'Gd', 'Ex']]))]),
 'pipeline-3': Pipeline(steps=[('simpleimputer', SimpleImputer(strategy='most_frequent')),
                 ('ordinalencoder',
                  OrdinalEncoder(categories=[['NA', 'No', 'Mn', 'Av', 'Gd'],
                                             ['NA', 'Unf', 'LwQ', 'Rec', 'BLQ',
                                              'ALQ', 'GLQ'],
                                             ['NA', 'Unf', 'LwQ', 'Rec', 'BLQ',
                                              'ALQ', 'GLQ'],
                                             ['Sal', 'Sev', 'Maj2', 'Maj1',
                                              'Mod', 'Min2', 'Min1', 'Typ'],
                                             ['NA', 'MnWw', 'GdWo', 'MnPrv',
                                              'GdPrv']]))]),
 'pipeline-4': Pipeline(steps=[('simpleimputer',
                  SimpleImputer(fill_value='missing', strategy='constant')),
                 ('onehotencoder',
                  OneHotEncoder(handle_unknown='ignore', sparse=False,
                                sparse_output=False))])}

ohe_columns = list(
    preprocessor.named_transformers_["pipeline-4"]
    .named_steps["onehotencoder"]
    .get_feature_names_out(categorical_features)
)
new_columns = (
    numeric_features + ordinal_features_reg + ordinal_features_oth + ohe_columns
)

X_train_enc = pd.DataFrame(
    preprocessor.transform(X_train), index=X_train.index, columns=new_columns
)
X_train_enc

	BedroomAbvGr	KitchenAbvGr	LotFrontage	LotArea	OverallQual	OverallCond	YearBuilt	YearRemodAdd	MasVnrArea	BsmtFinSF1	...	Foundation_PConc	Foundation_Slab	Foundation_Stone	Foundation_Wood	RoofStyle_Flat	RoofStyle_Gable	RoofStyle_Gambrel	RoofStyle_Hip	RoofStyle_Mansard	RoofStyle_Shed
302	0.154795	-0.222647	2.312501	0.381428	0.663680	-0.512408	0.993969	0.840492	0.269972	-0.961498	...	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
767	1.372763	-0.222647	0.260890	0.248457	-0.054669	1.285467	-1.026793	0.016525	-0.573129	0.476092	...	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
429	0.154795	-0.222647	2.885044	0.131607	-0.054669	-0.512408	0.563314	0.161931	-0.573129	1.227559	...	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
1139	0.154795	-0.222647	1.358264	-0.171468	-0.773017	-0.512408	-1.689338	-1.679877	-0.573129	0.443419	...	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
558	0.154795	-0.222647	-0.597924	1.289541	0.663680	-0.512408	0.828332	0.598149	-0.573129	0.354114	...	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
1041	1.372763	-0.222647	-0.025381	-0.127107	-0.054669	2.184405	-0.165485	0.743555	0.843281	-0.090231	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0
1122	0.154795	-0.222647	-0.025381	-0.149788	-1.491366	-2.310284	-0.496757	-1.389065	-0.573129	-0.961498	...	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
1346	0.154795	-0.222647	-0.025381	1.168244	0.663680	1.285467	-0.099230	0.888961	-0.573129	-0.314582	...	0.0	0.0	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0
1406	-1.063173	-0.222647	0.022331	-0.203265	-0.773017	1.285467	0.033279	1.082835	-0.573129	0.467379	...	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0
1389	0.154795	-0.222647	-0.454788	-0.475099	-0.054669	0.386530	-0.993666	-1.679877	-0.573129	-0.144686	...	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0

1314 rows × 262 columns

X_train_enc.shape

(1314, 262)

lr_pipe = make_pipeline(preprocessor, Ridge())
scores = cross_validate(lr_pipe, X_train, y_train, return_train_score=True)
pd.DataFrame(scores)

	fit_time	score_time	test_score	train_score
0	0.029269	0.007910	0.835749	0.916722
1	0.025759	0.007089	0.810073	0.919198
2	0.024959	0.006794	0.831611	0.912395
3	0.024889	0.006736	0.843992	0.914003
4	0.024066	0.008359	0.548831	0.920462

Feature importances#

How does the output depend upon the input?
How do the predictions change as a function of a particular feature?
If the model is bad interpretability does not make sense.

SimpleFeature correlations#

Let’s look at the correlations between various features with other features and the target in our encoded data (first row/column).
In simple terms here is how you can interpret correlations between two variables $X$ and $Y$:
- If $Y$ goes up when $X$ goes up, we say $X$ and $Y$ are positively correlated.
- If $Y$ goes down when $X$ goes up, we say $X$ and $Y$ are negatively correlated.
- If $Y$ is unchanged when $X$ changes, we say $X$ and $Y$ are uncorrelated.

Let’s examine the correlations among different columns, including the target column.

cor = pd.concat((y_train, X_train_enc), axis=1).iloc[:, :10].corr()
plt.figure(figsize=(8, 6))
sns.set(font_scale=0.8)
sns.heatmap(cor, annot=True, cmap=plt.cm.Blues);

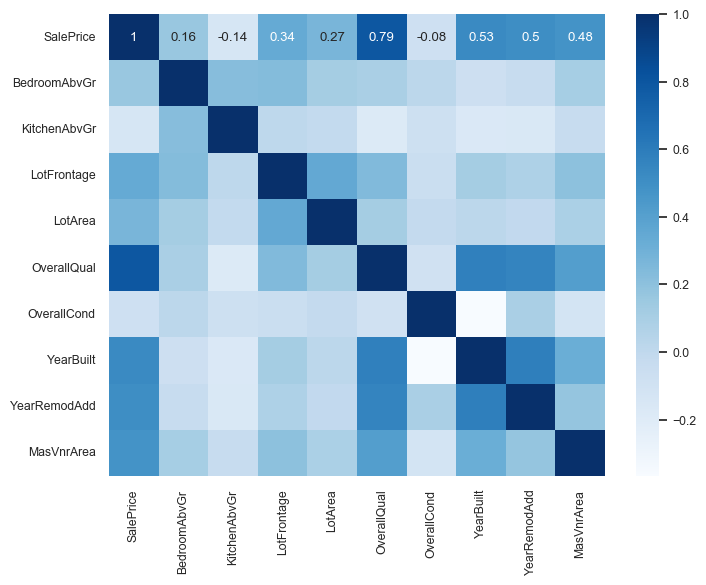
../_images/08bb0634c6f5a8594083eb48b234459243307febb22faeab0b06c7d7d8982ae8.png

We can immediately see that SalePrice is highly correlated with OverallQual.
This is an early hint that OverallQual is a useful feature in predicting SalePrice.
However, this approach is extremely simplistic.
- It only looks at each feature in isolation.
- It only looks at linear associations:
  - What if SalePrice is high when BsmtFullBath is 2 or 3, but low when it’s 0, 1, or 4? They might seem uncorrelated.

cor = pd.concat((y_train, X_train_enc), axis=1).iloc[:, 10:15].corr()
plt.figure(figsize=(4, 4))
sns.set(font_scale=0.8)
sns.heatmap(cor, annot=True, cmap=plt.cm.Blues);

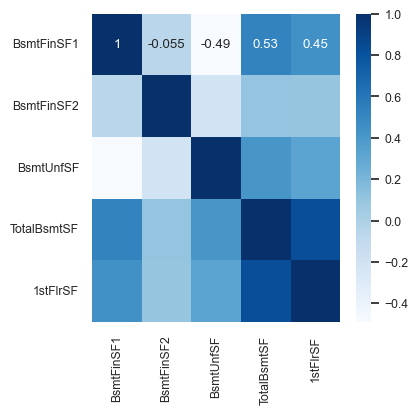
../_images/425cbe3f8410fb4dbf4398bed212e135fafad7571cece542713299e433f8b202.png

Looking at this diagram also tells us the relationship between features.
- For example, 1stFlrSF and TotalBsmtSF are highly correlated.
- Do we need both of them?
- If our model says 1stFlrSF is very important and TotalBsmtSF is very unimportant, do we trust those values?
- Maybe TotalBsmtSF only “becomes important” if 1stFlrSF is removed.
- Sometimes the opposite happens: a feature only becomes important if another feature is added.

Feature importances in linear models#

With linear regression we can look at the coefficients for each feature.
Overall idea: predicted price = intercept + $\sum_i$ coefficient i $\times$ feature i.

lr = make_pipeline(preprocessor, Ridge())
lr.fit(X_train, y_train);

Let’s look at the coefficients.

lr_coefs = pd.DataFrame(
    data=lr.named_steps["ridge"].coef_, index=new_columns, columns=["Coefficient"]
)
lr_coefs.head(20)

	Coefficient
BedroomAbvGr	-3717.542624
KitchenAbvGr	-4552.332671
LotFrontage	-1582.710031
LotArea	5118.035161
OverallQual	12498.401830
OverallCond	4854.438906
YearBuilt	4234.888066
YearRemodAdd	317.185155
MasVnrArea	5253.253432
BsmtFinSF1	3681.749118
BsmtFinSF2	581.237935
BsmtUnfSF	-1273.072243
TotalBsmtSF	2759.043319
1stFlrSF	6744.462545
2ndFlrSF	13407.646050
LowQualFinSF	-447.627722
GrLivArea	15992.080694
BsmtFullBath	2305.121599
BsmtHalfBath	500.215865
FullBath	2836.007434

Let’s try to interpret coefficients for different types of features.

Ordinal features#

The ordinal features are easiest to interpret.

print(ordinal_features_reg)

['ExterQual', 'ExterCond', 'BsmtQual', 'BsmtCond', 'HeatingQC', 'KitchenQual', 'FireplaceQu', 'GarageQual', 'GarageCond', 'PoolQC']

lr_coefs.loc["ExterQual"]

Coefficient    4236.969653
Name: ExterQual, dtype: float64

Increasing by one category of exterior quality (e.g. good -> excellent) increases the predicted price by $\sim\$4195$.
- Wow, that’s a lot!
- Remember this is just what the model has learned. It doesn’t tell us how the world works.

one_example = X_test[:1]

one_example[["ExterQual"]]

	ExterQual
147	Gd

Let’s perturb the example and change ExterQual to Ex.

one_example_perturbed = one_example.copy()
one_example_perturbed["ExterQual"] = "Ex"  # Change Gd to Ex

one_example_perturbed[["ExterQual"]]

	ExterQual
147	Ex

How does the prediction change after changing ExterQual from Gd to Ex?

print("Prediction on the original example: ", lr.predict(one_example))
print("Prediction on the perturbed example: ", lr.predict(one_example_perturbed))
print(
    "After changing ExterQual from Gd to Ex increased the prediction by: ",
    lr.predict(one_example_perturbed) - lr.predict(one_example),
)

Prediction on the original example:  [224865.34161762]
Prediction on the perturbed example:  [229102.31127015]
After changing ExterQual from Gd to Ex increased the prediction by:  [4236.96965253]

That’s exactly the learned coefficient for ExterQual!

lr_coefs.loc["ExterQual"]

Coefficient    4236.969653
Name: ExterQual, dtype: float64

So our interpretation is correct!

Increasing by one category of exterior quality (e.g. good -> excellent) increases the predicted price by $\sim\$4195$.

Categorical features#

What about the categorical features?
We have created a number of columns for each category with OHE and each category gets it’s own coefficient.

print(categorical_features)

['Condition1', 'MSSubClass', 'LandSlope', 'SaleCondition', 'CentralAir', 'MoSold', 'Electrical', 'GarageFinish', 'Neighborhood', 'GarageType', 'Exterior1st', 'MiscFeature', 'Utilities', 'Condition2', 'MSZoning', 'BldgType', 'Heating', 'Street', 'LotConfig', 'Exterior2nd', 'MasVnrType', 'HouseStyle', 'Alley', 'SaleType', 'LandContour', 'LotShape', 'RoofMatl', 'PavedDrive', 'Foundation', 'RoofStyle']

lr_coefs_landslope = lr_coefs[lr_coefs.index.str.startswith("LandSlope")]
lr_coefs_landslope

	Coefficient
LandSlope_Gtl	468.638169
LandSlope_Mod	7418.923432
LandSlope_Sev	-7887.561602

We can talk about switching from one of these categories to another by picking a “reference” category:

lr_coefs_landslope - lr_coefs_landslope.loc["LandSlope_Gtl"]

	Coefficient
LandSlope_Gtl	0.000000
LandSlope_Mod	6950.285263
LandSlope_Sev	-8356.199771

If you change the category from LandSlope_Gtl to LandSlope_Mod the prediction price goes up by $\sim\$6963$
If you change the category from LandSlope_Gtl to LandSlope_Sev the prediction price goes down by $\sim\$8334$

Note that this might not make sense in the real world but this is what our model decided to learn given this small amount of data.

one_example = X_test[:1]
one_example[['LandSlope']]

	LandSlope
147	Gtl

Let’s perturb the example and change LandSlope to Mod.

one_example_perturbed = one_example.copy()
one_example_perturbed["LandSlope"] = "Mod"  # Change Gd to Ex

one_example_perturbed[["LandSlope"]]

	LandSlope
147	Mod

How does the prediction change after changing LandSlope from Gtl to Mod?

print("Prediction on the original example: ", lr.predict(one_example))
print("Prediction on the perturbed example: ", lr.predict(one_example_perturbed))
print(
    "After changing ExterQual from Gd to Ex increased the prediction by: ",
    lr.predict(one_example_perturbed) - lr.predict(one_example),
)

Prediction on the original example:  [224865.34161762]
Prediction on the perturbed example:  [231815.62688064]
After changing ExterQual from Gd to Ex increased the prediction by:  [6950.28526302]

Our interpretation above is correct!

lr_coefs.sort_values(by="Coefficient")

	Coefficient
RoofMatl_ClyTile	-191169.071745
Condition2_PosN	-105656.864205
Heating_OthW	-27263.223804
MSZoning_C (all)	-22001.877390
Exterior1st_ImStucc	-19422.775311
...	...
PoolQC	34182.041704
RoofMatl_CompShg	36525.193346
Neighborhood_NridgHt	37546.996765
Neighborhood_StoneBr	39931.371722
RoofMatl_WdShngl	83603.013120

262 rows × 1 columns

For example, the above coefficient says that “If the roof is made of clay or tile, the predicted price is \$191K less”?
Do we believe these interpretations??
- Do we believe this is how the predictions are being computed? Yes.
- Do we believe that this is how the world works? No.

Note

If you did drop='first' (we didn’t) then you already have a reference class, and all the values are with respect to that one. The interpretation depends on whether we did drop='first', hence the hassle.

Interpreting coefficients of numeric features#

Let’s look at coefficients of PoolArea, LotFrontage, LotArea.

lr_coefs.loc[["PoolArea", "LotFrontage", "LotArea"]]

	Coefficient
PoolArea	2817.196385
LotFrontage	-1582.710031
LotArea	5118.035161

Intuition:

Tricky because numeric features are scaled!
Increasing PoolArea by 1 scaled unit increases the predicted price by $\sim\$2822$.
Increasing LotArea by 1 scaled unit increases the predicted price by $\sim\$5109$.
Increasing LotFrontage by 1 scaled unit decreases the predicted price by $\sim\$1578$.

Does that sound reasonable?

For PoolArea and LotArea, yes.
For LotFrontage, that’s surprising. Something positive would have made more sense?

It might be the case that LotFrontage is correlated with some other variable, which might have a larger positive coefficient.

BTW, let’s make sure the predictions behave as expected:

Example showing how can we interpret coefficients of scaled features.#

What’s one scaled unit for LotArea?
The scaler subtracted the mean and divided by the standard deviation.
The division actually changed the scale!
For the unit conversion, we don’t care about the subtraction, but only the scaling.

scaler = preprocessor.named_transformers_["pipeline-1"]["standardscaler"]

lr_scales = pd.DataFrame(
    data=np.sqrt(scaler.var_), index=numeric_features, columns=["Scale"]
)
lr_scales.head()

	Scale
BedroomAbvGr	0.821040
KitchenAbvGr	0.218760
LotFrontage	20.959139
LotArea	8994.471032
OverallQual	1.392082

It seems like LotArea was divided by 8994.471032 sqft.

lr_coefs.loc[["LotArea"]]

	Coefficient
LotArea	5118.035161

The coefficient tells us that if we increase the scaled LotArea by one scaled unit the price would go up by $\approx\$5118$.
One scaled unit represents $\sim 8994$ sqft in the original scale.

Let’s examine whether this behaves as expected.

X_test_enc = pd.DataFrame(
    preprocessor.transform(X_test), index=X_test.index, columns=new_columns
)

one_ex_preprocessed = X_test_enc[:1]
one_ex_preprocessed

	BedroomAbvGr	KitchenAbvGr	LotFrontage	LotArea	OverallQual	OverallCond	YearBuilt	YearRemodAdd	MasVnrArea	BsmtFinSF1	...	Foundation_PConc	Foundation_Slab	Foundation_Stone	Foundation_Wood	RoofStyle_Flat	RoofStyle_Gable	RoofStyle_Gambrel	RoofStyle_Hip	RoofStyle_Mansard	RoofStyle_Shed
147	0.154795	-0.222647	-0.025381	-0.085415	0.66368	-0.512408	0.993969	0.792023	0.438592	-0.961498	...	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0

1 rows × 262 columns

orig_pred = lr.named_steps["ridge"].predict(one_ex_preprocessed)
orig_pred

/Users/kvarada/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/base.py:458: UserWarning: X has feature names, but Ridge was fitted without feature names
  warnings.warn(

array([224865.34161762])

one_ex_preprocessed_perturbed = one_ex_preprocessed.copy()
one_ex_preprocessed_perturbed["LotArea"] += 1  # we are adding one to the scaled LotArea
one_ex_preprocessed_perturbed

	BedroomAbvGr	KitchenAbvGr	LotFrontage	LotArea	OverallQual	OverallCond	YearBuilt	YearRemodAdd	MasVnrArea	BsmtFinSF1	...	Foundation_PConc	Foundation_Slab	Foundation_Stone	Foundation_Wood	RoofStyle_Flat	RoofStyle_Gable	RoofStyle_Gambrel	RoofStyle_Hip	RoofStyle_Mansard	RoofStyle_Shed
147	0.154795	-0.222647	-0.025381	0.914585	0.66368	-0.512408	0.993969	0.792023	0.438592	-0.961498	...	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0	0.0	0.0

1 rows × 262 columns

We are expecting an increase of $5118.03516073 in the prediction compared to the original value of LotArea.

perturbed_pred = lr.named_steps["ridge"].predict(one_ex_preprocessed_perturbed)

/Users/kvarada/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/base.py:458: UserWarning: X has feature names, but Ridge was fitted without feature names
  warnings.warn(

perturbed_pred - orig_pred

array([5118.03516073])

Our interpretation is correct!

Humans find it easier to think about features in their original scale.
How can we interpret this coefficient in the original scale?
If I increase original LotArea by one square foot then the predicted price would go up by this amount:

5118.03516073 / 8994.471032 # Coefficient learned on the scaled features / the scaling factor for this feature

0.5690201394302518

one_example = X_test[:1]

one_example

	Id	MSSubClass	MSZoning	LotFrontage	LotArea	Street	Alley	LotShape	LandContour	Utilities	...	ScreenPorch	PoolArea	PoolQC	Fence	MiscFeature	MiscVal	MoSold	YrSold	SaleType	SaleCondition
147	148	60	RL	NaN	9505	Pave	NaN	IR1	Lvl	AllPub	...	0	0	NaN	NaN	NaN	0	5	2010	WD	Normal

1 rows × 80 columns

Let’s perturb the example and add 1 to the LotArea.

one_example_perturbed = one_example.copy()
one_example_perturbed["LotArea"] += 1

if we add 8994.471032 to the original LotArea, the housing price prediction should go up by the coefficient 5109.35671794.

one_example_perturbed

	Id	MSSubClass	MSZoning	LotFrontage	LotArea	Street	Alley	LotShape	LandContour	Utilities	...	ScreenPorch	PoolArea	PoolQC	Fence	MiscFeature	MiscVal	MoSold	YrSold	SaleType	SaleCondition
147	148	60	RL	NaN	9506	Pave	NaN	IR1	Lvl	AllPub	...	0	0	NaN	NaN	NaN	0	5	2010	WD	Normal

1 rows × 80 columns

Prediction on the original example.

lr.predict(one_example)

array([224865.34161762])

Prediction on the perturbed example.

lr.predict(one_example_perturbed)

array([224865.91063776])

What’s the difference between predictions?
Does the difference make sense given the coefficient of the feature?

lr.predict(one_example_perturbed) - lr.predict(one_example)

array([0.56902014])

Yes! Our interpretation is correct.

That said don’t read too much into these coefficients without statistical training.

Interim summary#

Correlation among features might make coefficients completely uninterpretable.
Fairly straightforward to interpret coefficients of ordinal features.
In categorical features, it’s often helpful to consider one category as a reference point and think about relative importance.
For numeric features, relative importance is meaningful after scaling.
You have to be careful about the scale of the feature when interpreting the coefficients.
Remember that explaining the model $\neq$ explaining the data or explaining how the world works.
The coefficients tell us only about the model and they might not accurately reflect the data.

Transparency and explainability of ML models: Motivation#

Activity (~5 mins)#

Suppose you have a machine learning model which gives you a 98% cross-validation score (with the metric of your interest) and 97% test score on a reasonably sized train and test sets. Since you have impressive cross-validation and test scores, you decide to just trust the model and use it as a black box, ignoring why it’s making certain predictions.

Give some scenarios when this might or might not be problematic. Write your thoughts in this Google document.

Why model transparency/interpretability?#

Ability to interpret ML models is crucial in many applications such as banking, healthcare, and criminal justice.
It can be leveraged by domain experts to diagnose systematic errors and underlying biases of complex ML systems.

Source

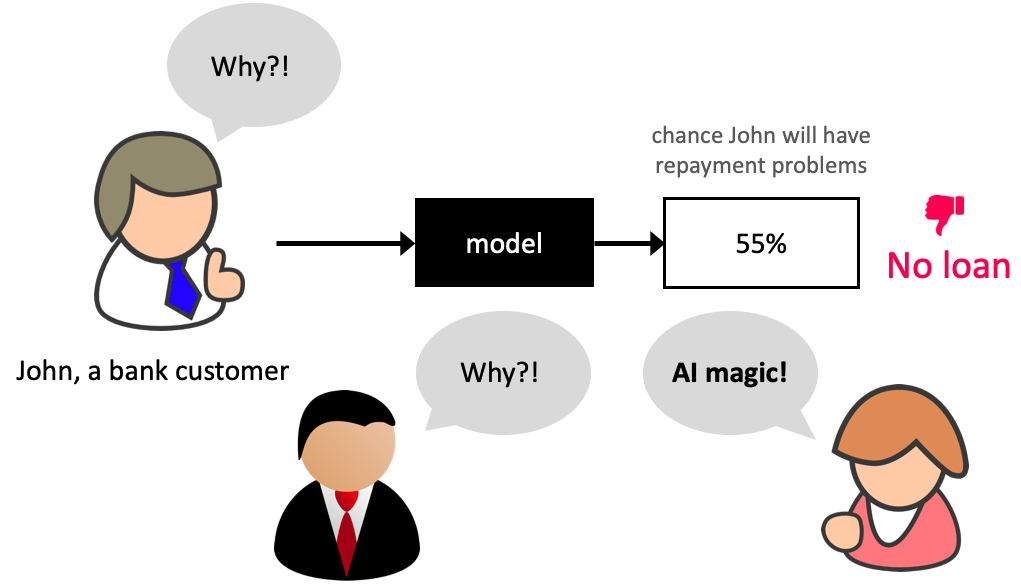
What is model interpretability?#

In this lecture, our definition of model interpretability will be looking at feature importances, i.e., exploring features which are important to the model.
There is more to interpretability than feature importances, but it’s a good start!
Resources:
- Interpretable Machine Learning
- Yann LeCun, Kilian Weinberger, Patrice Simard, and Rich Caruana: Panel debate on interpretability

Data#

Let’s work with the adult census data set from the last lecture.

adult_df_large = pd.read_csv("data/adult.csv")
train_df, test_df = train_test_split(adult_df_large, test_size=0.2, random_state=42)
train_df_nan = train_df.replace("?", np.NaN)
test_df_nan = test_df.replace("?", np.NaN)
train_df_nan.head()

	age	workclass	fnlwgt	education	education.num	marital.status	occupation	relationship	race	sex	hours.per.week	native.country	income
5514	26	Private	256263	HS-grad	9	Never-married	Craft-repair	Not-in-family	White	Male	25	United-States	<=50K
19777	24	Private	170277	HS-grad	9	Never-married	Other-service	Not-in-family	White	Female	35	United-States	<=50K
10781	36	Private	75826	Bachelors	13	Divorced	Adm-clerical	Unmarried	White	Female	40	United-States	<=50K
32240	22	State-gov	24395	Some-college	10	Married-civ-spouse	Adm-clerical	Wife	White	Female	20	United-States	<=50K
9876	31	Local-gov	356689	Bachelors	13	Married-civ-spouse	Prof-specialty	Husband	White	Male	40	United-States	<=50K

numeric_features = ["age", "capital.gain", "capital.loss", "hours.per.week"]
categorical_features = [
    "workclass",
    "marital.status",
    "occupation",
    "relationship",
    "native.country",
]
ordinal_features = ["education"]
binary_features = ["sex"]
drop_features = ["race", "education.num", "fnlwgt"]
target_column = "income"

education_levels = [
    "Preschool",
    "1st-4th",
    "5th-6th",
    "7th-8th",
    "9th",
    "10th",
    "11th",
    "12th",
    "HS-grad",
    "Prof-school",
    "Assoc-voc",
    "Assoc-acdm",
    "Some-college",
    "Bachelors",
    "Masters",
    "Doctorate",
]

assert set(education_levels) == set(train_df["education"].unique())

numeric_transformer = make_pipeline(SimpleImputer(strategy="median"), StandardScaler())
tree_numeric_transformer = make_pipeline(SimpleImputer(strategy="median"))

categorical_transformer = make_pipeline(
    SimpleImputer(strategy="constant", fill_value="missing"),
    OneHotEncoder(handle_unknown="ignore"),
)

ordinal_transformer = make_pipeline(
    SimpleImputer(strategy="constant", fill_value="missing"),
    OrdinalEncoder(categories=[education_levels], dtype=int),
)

binary_transformer = make_pipeline(
    SimpleImputer(strategy="constant", fill_value="missing"),
    OneHotEncoder(drop="if_binary", dtype=int),
)

preprocessor = make_column_transformer(
    ("drop", drop_features),
    (numeric_transformer, numeric_features),
    (ordinal_transformer, ordinal_features),
    (binary_transformer, binary_features),
    (categorical_transformer, categorical_features),
)

X_train = train_df_nan.drop(columns=[target_column])
y_train = train_df_nan[target_column]

X_test = test_df_nan.drop(columns=[target_column])
y_test = test_df_nan[target_column]

# encode categorical class values as integers for XGBoost
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
y_train_num = label_encoder.fit_transform(y_train)
y_test_num = label_encoder.transform(y_test)

Do we have class imbalance?#

There is class imbalance. But without any context, both classes seem equally important.
Let’s use accuracy as our metric.

train_df_nan["income"].value_counts(normalize=True)

income
<=50K    0.757985
>50K     0.242015
Name: proportion, dtype: float64

scoring_metric = "accuracy"

Let’s store all the results in a dictionary called results.

results = {}

We are going to use models outside sklearn. Some of them cannot handle categorical target values. So we’ll convert them to integers using LabelEncoder.

y_train_num

array([0, 0, 0, ..., 1, 1, 0])

Baseline#

dummy = DummyClassifier()
results["Dummy"] = mean_std_cross_val_scores(
    dummy, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
)

Different models#

from lightgbm.sklearn import LGBMClassifier
from xgboost import XGBClassifier

pipe_lr = make_pipeline(
    preprocessor, LogisticRegression(max_iter=2000, random_state=123)
)
pipe_rf = make_pipeline(preprocessor, RandomForestClassifier(random_state=123))
pipe_xgb = make_pipeline(
    preprocessor, XGBClassifier(random_state=123, eval_metric="logloss", verbosity=0)
)
pipe_lgbm = make_pipeline(preprocessor, LGBMClassifier(random_state=123, verbose=-1))
classifiers = {
    "logistic regression": pipe_lr,
    "random forest": pipe_rf,
    "XGBoost": pipe_xgb,
    "LightGBM": pipe_lgbm,
}

for (name, model) in classifiers.items():
    results[name] = mean_std_cross_val_scores(
        model, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
    )

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[68], line 2
for (name, model) in classifiers.items():
----> 2     results[name] = mean_std_cross_val_scores(
       model, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
   )

File ~/CS/2023-24/330/cpsc330-2023W1/lectures/code/utils.py:79, in mean_std_cross_val_scores(model, X_train, y_train, **kwargs)
def mean_std_cross_val_scores(model, X_train, y_train, **kwargs):
   """
   Returns mean and std of cross validation

   (...)
       pandas Series with mean scores from cross_validation
   """
---> 79     scores = cross_validate(model, X_train, y_train, **kwargs)
   mean_scores = pd.DataFrame(scores).mean()
   std_scores = pd.DataFrame(scores).std()

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/utils/_param_validation.py:214, in validate_params.<locals>.decorator.<locals>.wrapper(*args, **kwargs)
try:
   with config_context(
       skip_parameter_validation=(
           prefer_skip_nested_validation or global_skip_validation
       )
   ):
--> 214         return func(*args, **kwargs)
except InvalidParameterError as e:
   # When the function is just a wrapper around an estimator, we allow
   # the function to delegate validation to the estimator, but we replace
   # the name of the estimator by the name of the function in the error
   # message to avoid confusion.
   msg = re.sub(
       r"parameter of \w+ must be",
       f"parameter of {func.__qualname__} must be",
       str(e),
   )

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/model_selection/_validation.py:309, in cross_validate(estimator, X, y, groups, scoring, cv, n_jobs, verbose, fit_params, pre_dispatch, return_train_score, return_estimator, return_indices, error_score)
# We clone the estimator to make sure that all the folds are
# independent, and that it is pickle-able.
parallel = Parallel(n_jobs=n_jobs, verbose=verbose, pre_dispatch=pre_dispatch)
--> 309 results = parallel(
   delayed(_fit_and_score)(
       clone(estimator),
       X,
       y,
       scorers,
       train,
       test,
       verbose,
       None,
       fit_params,
       return_train_score=return_train_score,
       return_times=True,
       return_estimator=return_estimator,
       error_score=error_score,
   )
   for train, test in indices
)
_warn_or_raise_about_fit_failures(results, error_score)
# For callable scoring, the return type is only know after calling. If the
# return type is a dictionary, the error scores can now be inserted with
# the correct key.

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/utils/parallel.py:65, in Parallel.__call__(self, iterable)
config = get_config()
iterable_with_config = (
   (_with_config(delayed_func, config), args, kwargs)
   for delayed_func, args, kwargs in iterable
)
---> 65 return super().__call__(iterable_with_config)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/joblib/parallel.py:1863, in Parallel.__call__(self, iterable)
   output = self._get_sequential_output(iterable)
   next(output)
-> 1863     return output if self.return_generator else list(output)
# Let's create an ID that uniquely identifies the current call. If the
# call is interrupted early and that the same instance is immediately
# re-used, this id will be used to prevent workers that were
# concurrently finalizing a task from the previous call to run the
# callback.
with self._lock:

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/joblib/parallel.py:1792, in Parallel._get_sequential_output(self, iterable)
self.n_dispatched_batches += 1
self.n_dispatched_tasks += 1
-> 1792 res = func(*args, **kwargs)
self.n_completed_tasks += 1
self.print_progress()

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/utils/parallel.py:127, in _FuncWrapper.__call__(self, *args, **kwargs)
   config = {}
with config_context(**config):
--> 127     return self.function(*args, **kwargs)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/model_selection/_validation.py:729, in _fit_and_score(estimator, X, y, scorer, train, test, verbose, parameters, fit_params, return_train_score, return_parameters, return_n_test_samples, return_times, return_estimator, split_progress, candidate_progress, error_score)
       estimator.fit(X_train, **fit_params)
   else:
--> 729         estimator.fit(X_train, y_train, **fit_params)
except Exception:
   # Note fit time as time until error
   fit_time = time.time() - start_time

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/base.py:1152, in _fit_context.<locals>.decorator.<locals>.wrapper(estimator, *args, **kwargs)
   estimator._validate_params()
with config_context(
   skip_parameter_validation=(
       prefer_skip_nested_validation or global_skip_validation
   )
):
-> 1152     return fit_method(estimator, *args, **kwargs)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/pipeline.py:427, in Pipeline.fit(self, X, y, **fit_params)
   if self._final_estimator != "passthrough":
       fit_params_last_step = fit_params_steps[self.steps[-1][0]]
--> 427         self._final_estimator.fit(Xt, y, **fit_params_last_step)
return self

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/base.py:1152, in _fit_context.<locals>.decorator.<locals>.wrapper(estimator, *args, **kwargs)
   estimator._validate_params()
with config_context(
   skip_parameter_validation=(
       prefer_skip_nested_validation or global_skip_validation
   )
):
-> 1152     return fit_method(estimator, *args, **kwargs)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/ensemble/_forest.py:456, in BaseForest.fit(self, X, y, sample_weight)
trees = [
   self._make_estimator(append=False, random_state=random_state)
   for i in range(n_more_estimators)
]
# Parallel loop: we prefer the threading backend as the Cython code
# for fitting the trees is internally releasing the Python GIL
# making threading more efficient than multiprocessing in
# that case. However, for joblib 0.12+ we respect any
# parallel_backend contexts set at a higher level,
# since correctness does not rely on using threads.
--> 456 trees = Parallel(
   n_jobs=self.n_jobs,
   verbose=self.verbose,
   prefer="threads",
)(
   delayed(_parallel_build_trees)(
       t,
       self.bootstrap,
       X,
       y,
       sample_weight,
       i,
       len(trees),
       verbose=self.verbose,
       class_weight=self.class_weight,
       n_samples_bootstrap=n_samples_bootstrap,
   )
   for i, t in enumerate(trees)
)
# Collect newly grown trees
self.estimators_.extend(trees)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/utils/parallel.py:65, in Parallel.__call__(self, iterable)
config = get_config()
iterable_with_config = (
   (_with_config(delayed_func, config), args, kwargs)
   for delayed_func, args, kwargs in iterable
)
---> 65 return super().__call__(iterable_with_config)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/joblib/parallel.py:1863, in Parallel.__call__(self, iterable)
   output = self._get_sequential_output(iterable)
   next(output)
-> 1863     return output if self.return_generator else list(output)
# Let's create an ID that uniquely identifies the current call. If the
# call is interrupted early and that the same instance is immediately
# re-used, this id will be used to prevent workers that were
# concurrently finalizing a task from the previous call to run the
# callback.
with self._lock:

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/joblib/parallel.py:1792, in Parallel._get_sequential_output(self, iterable)
self.n_dispatched_batches += 1
self.n_dispatched_tasks += 1
-> 1792 res = func(*args, **kwargs)
self.n_completed_tasks += 1
self.print_progress()

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/utils/parallel.py:127, in _FuncWrapper.__call__(self, *args, **kwargs)
   config = {}
with config_context(**config):
--> 127     return self.function(*args, **kwargs)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/ensemble/_forest.py:188, in _parallel_build_trees(tree, bootstrap, X, y, sample_weight, tree_idx, n_trees, verbose, class_weight, n_samples_bootstrap)
   elif class_weight == "balanced_subsample":
       curr_sample_weight *= compute_sample_weight("balanced", y, indices=indices)
--> 188     tree.fit(X, y, sample_weight=curr_sample_weight, check_input=False)
else:
   tree.fit(X, y, sample_weight=sample_weight, check_input=False)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/base.py:1152, in _fit_context.<locals>.decorator.<locals>.wrapper(estimator, *args, **kwargs)
   estimator._validate_params()
with config_context(
   skip_parameter_validation=(
       prefer_skip_nested_validation or global_skip_validation
   )
):
-> 1152     return fit_method(estimator, *args, **kwargs)

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/tree/_classes.py:959, in DecisionTreeClassifier.fit(self, X, y, sample_weight, check_input)
@_fit_context(prefer_skip_nested_validation=True)
def fit(self, X, y, sample_weight=None, check_input=True):
   """Build a decision tree classifier from the training set (X, y).

   Parameters
   (...)
       Fitted estimator.
   """
--> 959     super()._fit(
       X,
       y,
       sample_weight=sample_weight,
       check_input=check_input,
   )
   return self

File ~/miniconda3/envs/cpsc330/lib/python3.10/site-packages/sklearn/tree/_classes.py:443, in BaseDecisionTree._fit(self, X, y, sample_weight, check_input, missing_values_in_feature_mask)
else:
   builder = BestFirstTreeBuilder(
       splitter,
       min_samples_split,
   (...)
       self.min_impurity_decrease,
   )
--> 443 builder.build(self.tree_, X, y, sample_weight, missing_values_in_feature_mask)
if self.n_outputs_ == 1 and is_classifier(self):
   self.n_classes_ = self.n_classes_[0]

KeyboardInterrupt: 

pd.DataFrame(results).T

	fit_time	score_time	test_score	train_score
Dummy	0.002 (+/- 0.000)	0.001 (+/- 0.000)	0.758 (+/- 0.000)	0.758 (+/- 0.000)
logistic regression	0.708 (+/- 0.056)	0.011 (+/- 0.001)	0.849 (+/- 0.005)	0.850 (+/- 0.001)
random forest	7.214 (+/- 0.083)	0.087 (+/- 0.010)	0.847 (+/- 0.006)	0.979 (+/- 0.000)
XGBoost	0.564 (+/- 0.014)	0.017 (+/- 0.002)	0.870 (+/- 0.004)	0.898 (+/- 0.001)
LightGBM	0.162 (+/- 0.024)	0.022 (+/- 0.002)	0.872 (+/- 0.004)	0.888 (+/- 0.000)

Logistic regression is giving reasonable scores but not the best ones.
XGBoost and LightGBM are giving us the best CV scores.

Often simple models (e.g., linear models) are interpretable but not very accurate.
Complex models (e.g., LightGBM) are more accurate but less interpretable.

Source

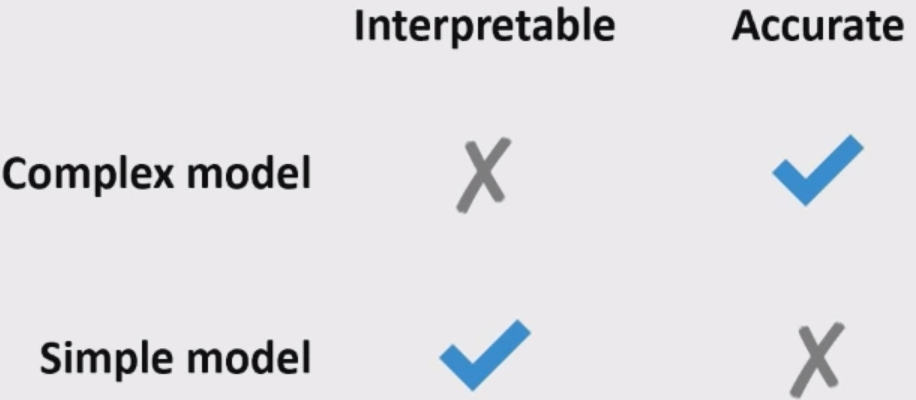
Feature importances in linear models#

Let’s create and fit a pipeline with preprocessor and logistic regression.

pipe_lr = make_pipeline(preprocessor, LogisticRegression(max_iter=2000, random_state=2))
pipe_lr.fit(X_train, y_train_num);

ohe_feature_names = (
    pipe_rf.named_steps["columntransformer"]
    .named_transformers_["pipeline-4"]
    .named_steps["onehotencoder"]
    .get_feature_names_out(categorical_features)
    .tolist()
)
feature_names = (
    numeric_features + ordinal_features + binary_features + ohe_feature_names
)
feature_names[:15]

['age',
 'capital.gain',
 'capital.loss',
 'hours.per.week',
 'education',
 'sex',
 'workclass_Federal-gov',
 'workclass_Local-gov',
 'workclass_Never-worked',
 'workclass_Private',
 'workclass_Self-emp-inc',
 'workclass_Self-emp-not-inc',
 'workclass_State-gov',
 'workclass_Without-pay',
 'workclass_missing']

data = {
    "coefficient": pipe_lr.named_steps["logisticregression"].coef_.flatten().tolist(),
    "magnitude": np.absolute(
        pipe_lr.named_steps["logisticregression"].coef_.flatten().tolist()
    ),
}
coef_df = pd.DataFrame(data, index=feature_names).sort_values(
    "magnitude", ascending=False
)

coef_df[:10]

	coefficient	magnitude
capital.gain	2.355921	2.355921
marital.status_Married-AF-spouse	1.752323	1.752323
occupation_Priv-house-serv	-1.426524	1.426524
marital.status_Married-civ-spouse	1.335259	1.335259
relationship_Wife	1.274059	1.274059
native.country_Columbia	-1.086099	1.086099
occupation_Prof-specialty	1.070978	1.070978
occupation_Exec-managerial	1.048124	1.048124
native.country_Dominican-Republic	-1.015952	1.015952
relationship_Own-child	-1.001010	1.001010

Increasing capital.gain is likely to push the prediction towards “>50k” income class
Whereas occupation of private house service is likely to push the prediction towards “<=50K” income.

Can we get feature importances for non-linear models?

Model interpretability beyond linear models#

We will be looking at interpretability in terms of feature importances.
Note that there is no absolute or perfect way to get feature importances. But it’s useful to get some idea on feature importances. So we just try our best.

We will be looking at two ways to get feature importances.

sklearn’s feature_importances_ and permutation_importance
SHAP

`sklearn`’s `feature_importances_` and `permutation_importance`#

Feature importance or variable importance is a score associated with a feature which tells us how “important” the feature is to the model.

Activity (~5 mins)#

Linear models learn a coefficient associated with each feature which tells us the importance of the feature to the model.

What might be some reasonable ways to calculate feature importances of the following models?
- Decision trees
- Linear SVMs
- KNNs, RBF SVMs
Suppose you have correlated features in your dataset. Do you need to be careful about this when you examine feature importances?

Discuss with your neighbour and write your ideas in this Google doc.

Do we have correlated features?#

X_train_enc = preprocessor.fit_transform(X_train).todense()
corr_df = pd.DataFrame(X_train_enc, columns=feature_names).corr().abs()

corr_df[corr_df == 1] = 0 # Set the diagonal to 0. 

Let’s look at columns where any correlation number is > 0.80.
0.80 is an arbitrary choice

high_corr = [column for column in corr_df.columns if any(corr_df[column] > 0.80)]
print(high_corr)

['workclass_missing', 'marital.status_Married-civ-spouse', 'occupation_missing', 'relationship_Husband']

Seems like there are some columns which are highly correlated.

corr_df['occupation_missing']['workclass_missing']

0.9977957422135846

corr_df['marital.status_Married-civ-spouse']['relationship_Husband']

0.8937442459553657

When we look at the feature importances, we should be mindful of these correlated features.
Remember the limitations of looking at simple linear correlations.
You should probably investigate multi-colinearity with more sophisticated approaches (e.g., variance inflation factors (VIF) from DSCI 561).

`sklearn`’s `feature_importances_` attribute vs `permutation_importance`#

Feature importances can be
- algorithm dependent, i.e., calculated based on the information given by the model algorithm (e.g., gini importance)
- model agnostic (e.g., by measuring increase in prediction error after permuting feature values).
Different measures give insight into different aspects of your data and model.

Here you will find some drawbacks of using feature_importances_ attribute in the context of tree-based models.

Decision tree feature importances#

pipe_dt = make_pipeline(preprocessor, DecisionTreeClassifier(max_depth=3))
pipe_dt.fit(X_train, y_train_num);

data = {
    "Importance": pipe_dt.named_steps["decisiontreeclassifier"].feature_importances_,
}
pd.DataFrame(data=data, index=feature_names,).sort_values(
    by="Importance", ascending=False
)[:10]

	Importance
marital.status_Married-civ-spouse	0.543351
capital.gain	0.294855
education	0.160727
age	0.001068
native.country_Guatemala	0.000000
native.country_Iran	0.000000
native.country_India	0.000000
native.country_Hungary	0.000000
native.country_Hong	0.000000
native.country_Honduras	0.000000

custom_plot_tree(pipe_dt.named_steps["decisiontreeclassifier"], feature_names = feature_names, fontsize=10)

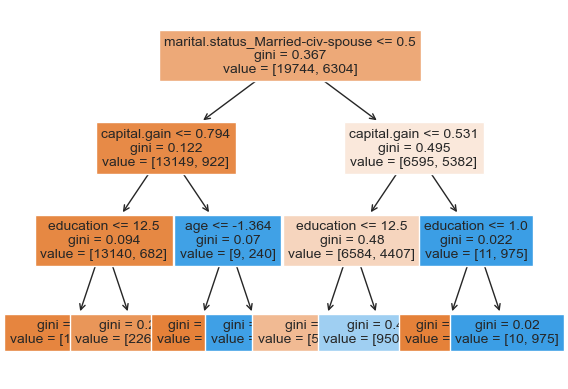
../_images/f45cb9ffbee5e01b59cf09a5c08039ca0765925cba8b765b9184df9d4e972ffb.png

Let’s explore permutation importance.

For each feature this method evaluates the impact of permuting feature values

from sklearn.inspection import permutation_importance
def get_permutation_importance(model):
    X_train_perm = X_train.drop(columns=["race", "education.num", "fnlwgt"])
    result = permutation_importance(model, X_train_perm, y_train_num, n_repeats=10, random_state=123)
    perm_sorted_idx = result.importances_mean.argsort()
    plt.boxplot(
        result.importances[perm_sorted_idx].T,
        vert=False,
        labels=X_train_perm.columns[perm_sorted_idx],
    )
    plt.xlabel('Permutation feature importance')
    plt.show()

get_permutation_importance(pipe_dt)

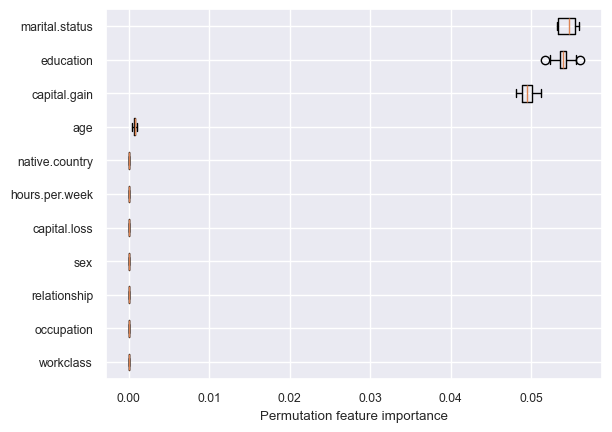
../_images/f3f8449f78b2a54c28ec5cb6f6035b19ffd76bbe4233856e898e87d33586b044.png

Decision tree is primarily making all decisions based on three features: marital.status, education, and capital.gain.

Let’s create and fit a pipeline with preprocessor and random forest.

Random forest feature importances#

pipe_rf = make_pipeline(preprocessor, RandomForestClassifier(random_state=2))
pipe_rf.fit(X_train, y_train_num);

Which features are driving the predictions the most?

data = {
    "Importance": pipe_rf.named_steps["randomforestclassifier"].feature_importances_,
}
rf_imp_df = pd.DataFrame(
    data=data,
    index=feature_names,
).sort_values(by="Importance", ascending=False)

rf_imp_df[:8]

	Importance
age	0.230412
education	0.122210
hours.per.week	0.114521
capital.gain	0.113815
marital.status_Married-civ-spouse	0.077887
relationship_Husband	0.044242
capital.loss	0.038287
marital.status_Never-married	0.025661

np.sum(pipe_rf.named_steps["randomforestclassifier"].feature_importances_)

0.9999999999999998

get_permutation_importance(pipe_rf)

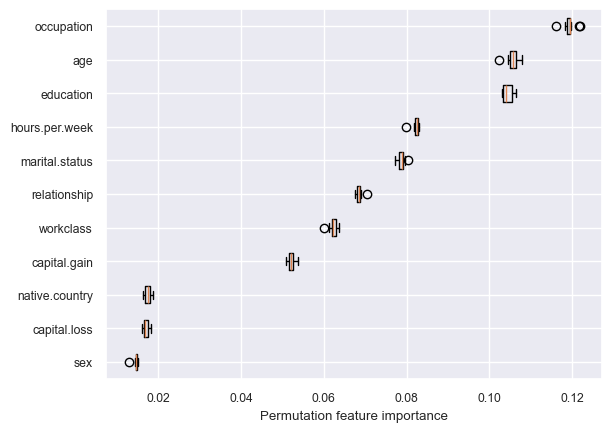
../_images/a417d7d60852ce17bd9a14dde3050f81f79a2355b34d1e6f169cbdd1a92e7f7d.png

Random forest is using more features in the model compared to decision trees.

Key point#

Unlike the linear model coefficients, feature_importances_ do not have a sign!
- They tell us about importance, but not an “up or down”.
- Indeed, increasing a feature may cause the prediction to first go up, and then go down.
- This cannot happen in linear models, because they are linear.

How can we get feature importances for non `sklearn` models?#

One way to do it is by using a tool called eli5.

Unfortunately, this is not compatible with the latest version of sklearn, which we are using.

conda install -c conda-forge eli5

Another popular way is using SHAP. You can install it using the following in the course conda environment.

conda install -c conda-forge shap

SHAP (SHapley Additive exPlanations) introduction#

Explaining a prediction#

Source

SHAP (SHapley Additive exPlanations)#

Based on the idea of shapely values. A shapely value is created for each example and each feature.
Can explain the prediction of an example by computing the contribution of each feature to the prediction.
Great visualizations
Support for different kinds of models; fast variants for tree-based models
Original paper: Lundberg and Lee, 2017

Our focus#

How to use it on our dataset?
How to generate and interpret plots created by SHAP?
We are not going to discuss how SHAP works.

Source

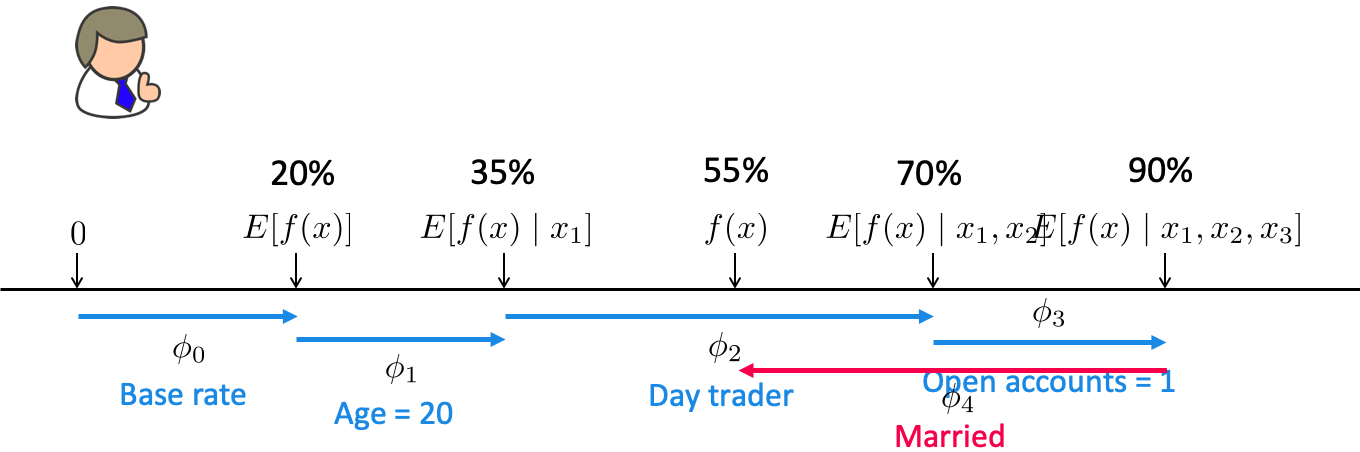
Start at a base rate (e.g., how often people get their loans rejected).
Add one feature at a time and see how it impacts the decision.

SHAP on LGBM model#

Let’s try it out on our best performing LightGBM model.
You should have shap in the course conda environment

Let’s create train and test dataframes with our transformed features.

X_train_enc = pd.DataFrame(
    data=preprocessor.transform(X_train).toarray(),
    columns=feature_names,
    index=X_train.index,
)
X_train_enc.head()

	age	capital.gain	capital.loss	hours.per.week	education	sex	workclass_Local-gov	workclass_Private	...	native.country_United-States
5514	-0.921955	-0.147166	-0.21768	-1.258387	8.0	1.0	0.0	1.0	...	1.0
19777	-1.069150	-0.147166	-0.21768	-0.447517	8.0	0.0	0.0	1.0	...	1.0
10781	-0.185975	-0.147166	-0.21768	-0.042081	13.0	0.0	0.0	1.0	...	1.0
32240	-1.216346	-0.147166	-0.21768	-1.663822	12.0	0.0	0.0	0.0	...	1.0
9876	-0.553965	-0.147166	-0.21768	-0.042081	13.0	1.0	1.0	0.0	...	1.0

5 rows × 85 columns

X_test_enc = pd.DataFrame(
    data=preprocessor.transform(X_test).toarray(),
    columns=feature_names,
    index=X_test.index,
)
X_test_enc.shape

(6513, 85)

Let’s get SHAP values for train and test data.

import shap

# Create a shap explainer object 
pipe_lgbm.named_steps["lgbmclassifier"].fit(X_train_enc, y_train)
lgbm_explainer = shap.TreeExplainer(pipe_lgbm.named_steps["lgbmclassifier"])
train_lgbm_shap_values = lgbm_explainer.shap_values(X_train_enc)

LightGBM binary classifier with TreeExplainer shap values output has changed to a list of ndarray

train_lgbm_shap_values

[array([[ 4.08151507e-01,  2.82025568e-01,  4.70162085e-02, ...,
         -1.03017665e-03,  0.00000000e+00, -1.69027185e-03],
        [ 5.46019608e-01,  2.77536150e-01,  4.69698010e-02, ...,
         -9.00720988e-04,  0.00000000e+00, -6.78058051e-04],
        [-4.39095422e-01,  2.50475372e-01,  6.51137414e-02, ...,
         -9.02446630e-04,  0.00000000e+00, -3.54676006e-04],
        ...,
        [-1.05137470e+00,  1.89706451e-01, -2.74798624e+00, ...,
         -1.13229595e-03,  0.00000000e+00, -1.31449687e-04],
        [-6.32247597e-01,  3.01432486e-01,  8.99744241e-02, ...,
         -1.03411038e-03,  0.00000000e+00,  4.04709519e-04],
        [ 1.15559528e+00,  2.32397724e-01,  5.55862988e-02, ...,
         -1.05290827e-03,  0.00000000e+00, -8.11336331e-04]]),
 array([[-4.08151507e-01, -2.82025568e-01, -4.70162085e-02, ...,
          1.03017665e-03,  0.00000000e+00,  1.69027185e-03],
        [-5.46019608e-01, -2.77536150e-01, -4.69698010e-02, ...,
          9.00720988e-04,  0.00000000e+00,  6.78058051e-04],
        [ 4.39095422e-01, -2.50475372e-01, -6.51137414e-02, ...,
          9.02446630e-04,  0.00000000e+00,  3.54676006e-04],
        ...,
        [ 1.05137470e+00, -1.89706451e-01,  2.74798624e+00, ...,
          1.13229595e-03,  0.00000000e+00,  1.31449687e-04],
        [ 6.32247597e-01, -3.01432486e-01, -8.99744241e-02, ...,
          1.03411038e-03,  0.00000000e+00, -4.04709519e-04],
        [-1.15559528e+00, -2.32397724e-01, -5.55862988e-02, ...,
          1.05290827e-03,  0.00000000e+00,  8.11336331e-04]])]

For each example, each feature, and each class we have a SHAP value.
SHAP values tell us how to fairly distribute the prediction among features.
For classification it’s a bit confusing. It gives SHAP matrix for all classes.
Let’s stick to shap values for class 1, i.e., income > 50K.

train_lgbm_shap_values[1].shape

(26048, 85)

test_lgbm_shap_values = lgbm_explainer.shap_values(X_test_enc)
test_lgbm_shap_values[1].shape

LightGBM binary classifier with TreeExplainer shap values output has changed to a list of ndarray

(6513, 85)

SHAP plots#

# load JS visualization code to notebook
shap.initjs()

Force plots#

Most useful!
Let’s try to explain predictions on a couple of examples from the test data.
I’m sampling some examples where target is <=50K and some examples where target is >50K.

y_test_reset = y_test.reset_index(drop=True)
y_test_reset

     <=50K
     <=50K
     <=50K
     <=50K
     <=50K
        ...  
  <=50K
  <=50K
   >50K
  <=50K
   >50K
Name: income, Length: 6513, dtype: object

l50k_ind = y_test_reset[y_test_reset == "<=50K"].index.tolist()
g50k_ind = y_test_reset[y_test_reset == ">50K"].index.tolist()

ex_l50k_index = l50k_ind[10]
ex_g50k_index = g50k_ind[10]

Explaining a prediction#

Imagine that you are given the following test example.

X_test_enc.iloc[ex_l50k_index]

age                               0.476406
capital.gain                     -0.147166
capital.loss                      4.649658
hours.per.week                   -0.042081
education                         8.000000
                                    ...   
native.country_Trinadad&Tobago    0.000000
native.country_United-States      1.000000
native.country_Vietnam            0.000000
native.country_Yugoslavia         0.000000
native.country_missing            0.000000
Name: 345, Length: 85, dtype: float64

You get the following hard prediction, which you are interested in explaining.

pipe_lgbm.named_steps["lgbmclassifier"].predict(X_test_enc)[ex_l50k_index]

'<=50K'

You can first look at predict_proba output to get a better understanding of model confidence.

pipe_lgbm.named_steps["lgbmclassifier"].predict_proba(X_test_enc)[ex_l50k_index]

array([0.99240562, 0.00759438])

The model seems quite confident. But if we want to know more, for example, which feature values are playing a role in this specific prediction, we can use SHAP force plots.
Remember that we have SHAP values per feature per example. We’ll use these values to create SHAP force plot.

pd.DataFrame(
    test_lgbm_shap_values[1][ex_l50k_index, :],
    index=feature_names,
    columns=["SHAP values"],
)

	SHAP values
age	0.723502
capital.gain	-0.253426
capital.loss	-0.256666
hours.per.week	-0.096692
education	-0.403715
...	...
native.country_Trinadad&Tobago	0.000000
native.country_United-States	0.003408
native.country_Vietnam	0.001051
native.country_Yugoslavia	0.000000
native.country_missing	0.000663

85 rows × 1 columns

SHAP will produce the following type of plots.

shap.force_plot(
    lgbm_explainer.expected_value[1], # expected value for class 1. 
    test_lgbm_shap_values[1][ex_l50k_index, :], # SHAP values associated with the example we want to explain
    X_test_enc.iloc[ex_l50k_index, :], # Feature vector of the example 
    matplotlib=True,
)

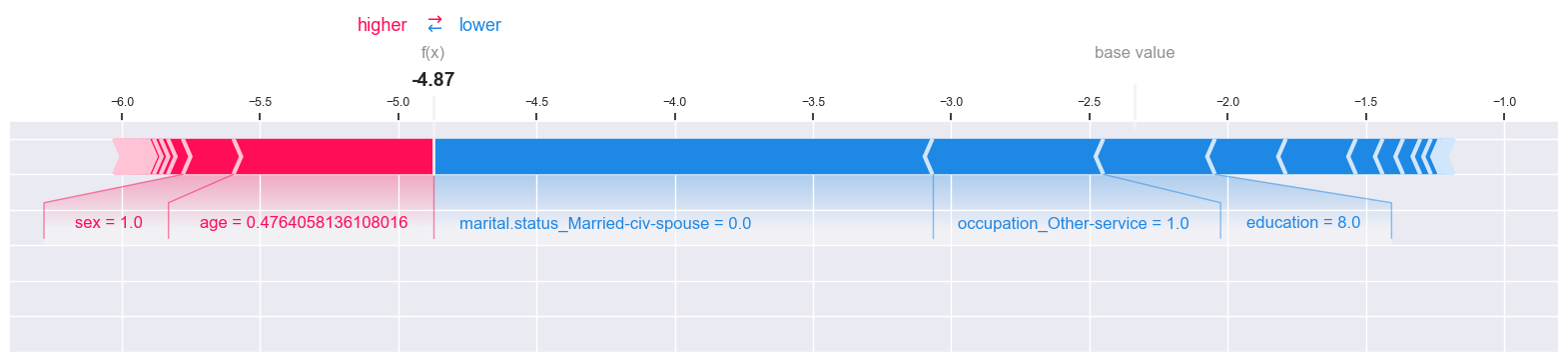
../_images/9adf6d15fd433026906ca9bcbb88b058b95b57b3b59bc6f5d91d44d00ee52ffd.png

The raw model score is much smaller than the base value, which is reflected in the prediction of <= 50k class.
sex = 1.0, scaled age = 0.48 are pushing the prediction towards higher score.
education = 8.0, occupation_Other-service = 1.0 and marital.status_Married-civ-spouse = 0.0 are pushing the prediction towards lower score.

pipe_lgbm.named_steps["lgbmclassifier"].classes_

array(['<=50K', '>50K'], dtype=object)

We can get the raw model output by passing raw_score=True in predict.

pipe_lgbm.named_steps["lgbmclassifier"].predict(X_test_enc, raw_score=True)

array([-1.76270194, -7.61912405, -0.45555535, ...,  1.13521135,
       -6.62873917, -0.84062193])

What’s the raw score of the example above we are trying to explain?

pipe_lgbm.named_steps["lgbmclassifier"].predict(X_test_enc, raw_score=True)[ex_l50k_index]

-4.872722908439952

The score matches with what we see in the force plot.
The base score above is the mean raw score. Our example has a lower raw score compared to the average raw score and the force plot tries to explain which feature values are bringing this score to a lower value.

pipe_lgbm.named_steps["lgbmclassifier"].predict(X_train_enc, raw_score=True).mean()

-2.336411423367732

lgbm_explainer.expected_value[1]  # on average this is the raw score for class 1

-2.3364114233677307

Note: a nice thing about SHAP values is that the feature importances sum to the prediction:

test_lgbm_shap_values[1][ex_l50k_index, :].sum() + lgbm_explainer.expected_value[1]

-4.8727229084399575

Now let’s try to explain another prediction.

The hard prediction here is 1.
From the predict_proba output it seems like the model is not too confident about the prediction.

pipe_lgbm.named_steps["lgbmclassifier"].predict(X_test_enc)[ex_g50k_index]

'>50K'

# X_test_enc.iloc[ex_g50k_index]

pipe_lgbm.named_steps["lgbmclassifier"].predict_proba(X_test_enc)[ex_g50k_index]

array([0.35997929, 0.64002071])

What’s the raw score for this example?

pipe_lgbm.named_steps["lgbmclassifier"].predict(X_test_enc, raw_score=True)[
    ex_g50k_index
]  # raw model score

0.5754540510801829

# pd.DataFrame(
#     test_lgbm_shap_values[1][ex_g50k_index, :],
#     index=feature_names,
#     columns=["SHAP values"],
# )

shap.force_plot(
    lgbm_explainer.expected_value[1],
    test_lgbm_shap_values[1][ex_g50k_index, :],
    X_test_enc.iloc[ex_g50k_index, :],
    matplotlib=True,
)

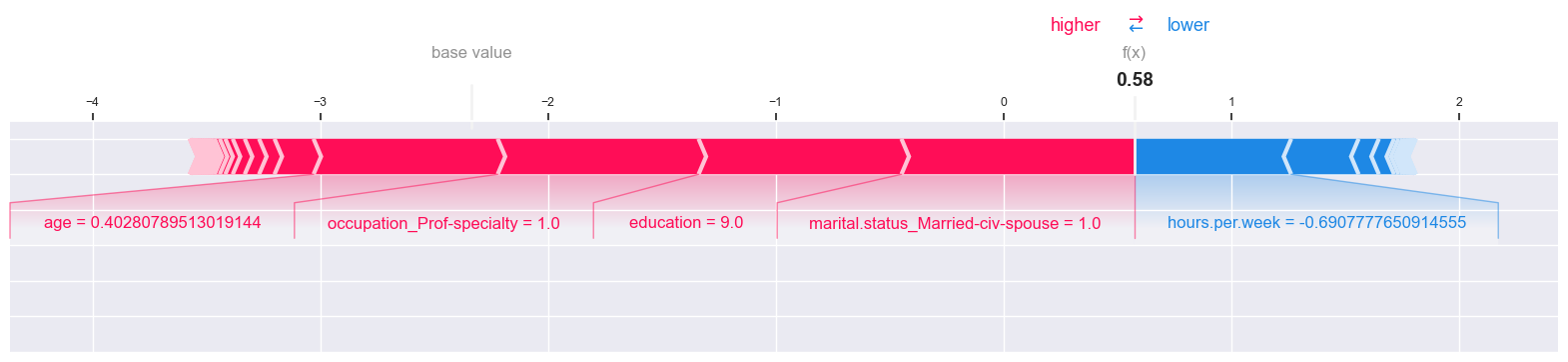
../_images/98ac8b5d5fc297d996a84171a9946fb4becea998e85634d544cbc597d3a541a4.png

Observations:

Everything is with respect to class 1 here.
The base value, i.e., the average raw score for class 1 is -2.336.
We see the forces that drive the prediction.
That is, we can see the main factors pushing it from the base value (average over the dataset) to this particular prediction.
Features that push the prediction to a higher value are shown in red.
Features that push the prediction to a lower value are shown in blue.

Global feature importance using SHAP#

Let’s look at the average SHAP values associated with each feature.

values = np.abs(train_lgbm_shap_values[1]).mean(
    0
)  # mean of shapely values in each column
pd.DataFrame(data=values, index=feature_names, columns=["SHAP"]).sort_values(
    by="SHAP", ascending=False
)[:10]

	SHAP
marital.status_Married-civ-spouse	1.074859
age	0.805468
capital.gain	0.565589
education	0.417642
hours.per.week	0.324636
sex	0.185687
capital.loss	0.148519
marital.status_Never-married	0.139914
relationship_Own-child	0.108003
occupation_Prof-specialty	0.106276

Dependence plot#

shap.dependence_plot("age", train_lgbm_shap_values[1], X_train_enc)

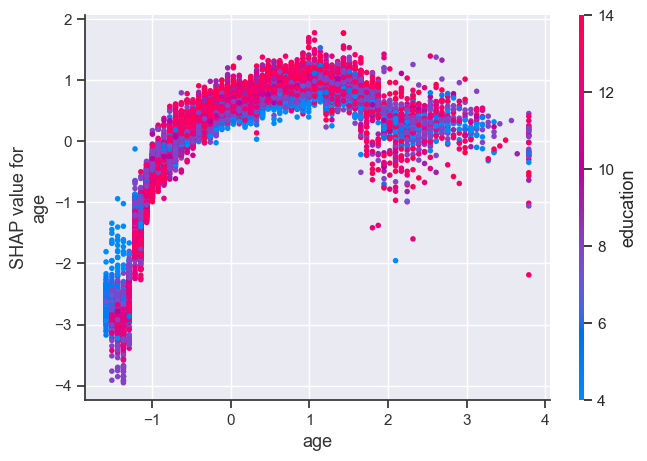
../_images/20ecb0892d29e714c142562f27af480528ef05431db543a3c806f62521c1c559.png

The plot above shows effect of age feature on the prediction.

Each dot is a single prediction for examples above.
The x-axis represents values of the feature age (scaled).
The y-axis is the SHAP value for that feature, which represents how much knowing that feature’s value changes the output of the model for that example’s prediction.
Lower values of age have smaller SHAP values for class “>50K”.
Similarly, higher values of age also have a bit smaller SHAP values for class “>50K”, which makes sense.
There is some optimal value of age between scaled age of 1 which gives highest SHAP values for for class “>50K”.
Ignore the colour for now. The color corresponds to a second feature (education feature in this case) that may have an interaction effect with the feature we are plotting.

Summary plot#

shap.summary_plot(train_lgbm_shap_values[1], X_train_enc)

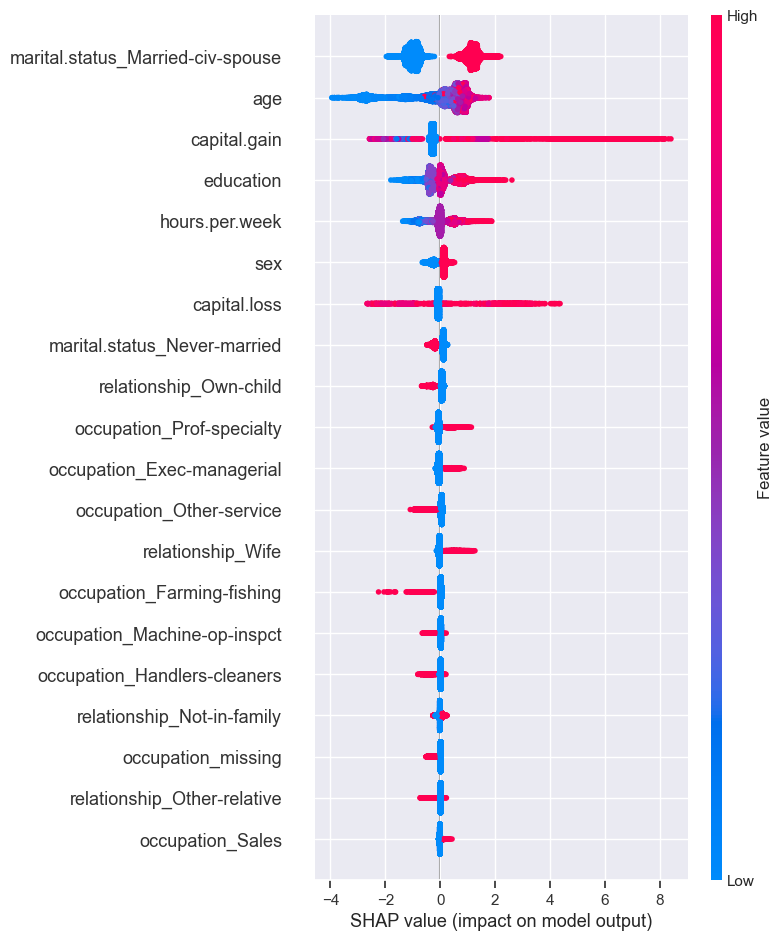
../_images/00e29a9b80cf41a3879e5a11e25e88c27c1ed099e41d58502f2d380cdb077b66.png

The plot shows the most important features for predicting the class. It also shows the direction of how it’s going to drive the prediction.

Presence of the marital status of Married-civ-spouse seems to have bigger SHAP values for class 1 and absence seems to have smaller SHAP values for class 1.
Higher levels of education seem to have bigger SHAP values for class 1 whereas smaller levels of education have smaller SHAP values.

shap.summary_plot(train_lgbm_shap_values[1], X_train_enc, plot_type="bar")

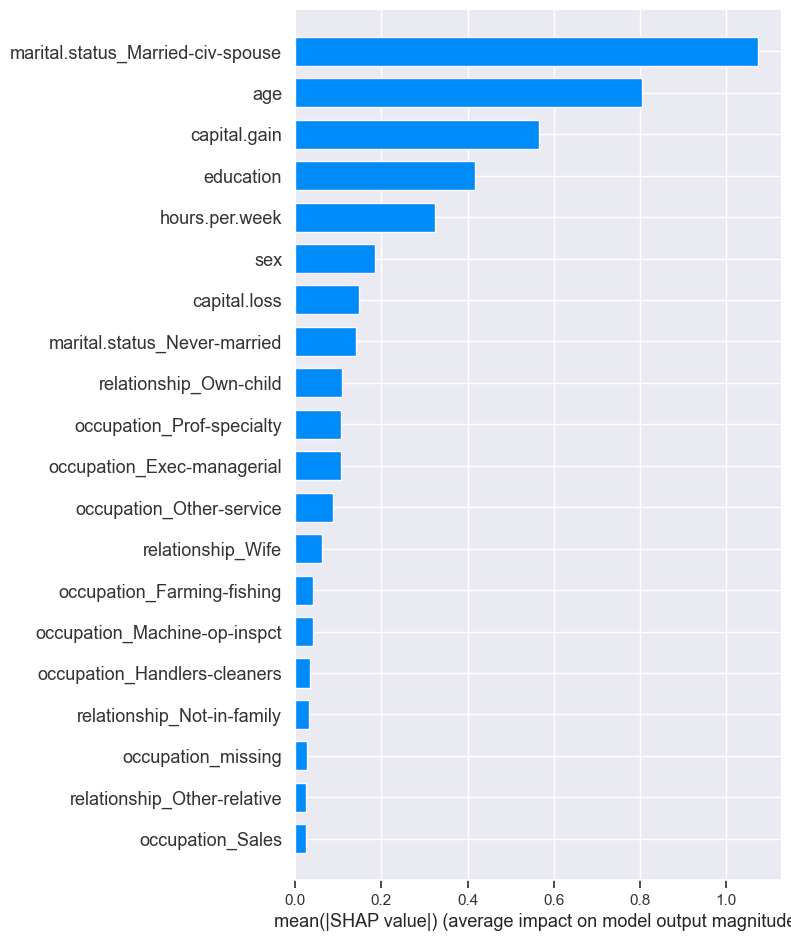
../_images/e51e97d8603108349d8db6924b309d82b7a54840749198e12bd4cada97fd5953.png

You can think of this as global feature importances.

Here, we explore SHAP’s TreeExplainer. It also provides explainer for different kinds of models.

TreeExplainer (supports XGBoost, CatBoost, LightGBM)
DeepExplainer (supports deep-learning models)
KernelExplainer (supports kernel-based models)
GradientExplainer (supports Keras and Tensorflow models)

Can also be used to explain text classification and image classification
Example: In the picture below, red pixels represent positive SHAP values that increase the probability of the class, while blue pixels represent negative SHAP values the reduce the probability of the class.

Source

Other tools#

lime is another package.

If you’re not already impressed, keep in mind:

So far we’ve only used sklearn models.
Most sklearn models have some built-in measure of feature importances.
On many tasks we need to move beyond sklearn, e.g. LightGBM, deep learning.
These tools work on other models as well, which makes them extremely useful.

Why do we want this information?#

Possible reasons:

Identify features that are not useful and maybe remove them.
Get guidance on what new data to collect.
- New features related to useful features -> better results.
- Don’t bother collecting useless features -> save resources.
Help explain why the model is making certain predictions.
- Debugging, if the model is behaving strangely.
- Regulatory requirements.
- Fairness / bias. See this.
- Keep in mind this can be used on deployment predictions!

Here are some guidelines and important points to remember when you work on a prediction problem where you also want to understand which features are influencing the predictions.

Examine multicoliniarity in your dataset using methods such as VIF.
If you observe high correlations in your dataset, either get rid of redundant features or be mindful of these correlations during interpretation.
Be mindful that feature relevance is not clearly defined. Adding/removing features can change feature importance/unimportance. Also, feature importances do not give us causal relationships. See this optional section from Lecture 4.
Most of the models we use in ML are regularized models. With L2 regularization, the feature importances are distributed evenly among correlated features. With L1 regularization, one of the correlated features gets a high importance and the other gets a lower importance.
Don’t be overconfident. Always take feature importance values with a grain of salt.

Lecture 12: Feature importances and model transparency

Contents

Lecture 12: Feature importances and model transparency#

Imports, announcements, LOs#

Imports#

Learning outcomes#

Announcement#

Data#

Let’s separate X and y#

Let’s identify feature types#

Feature importances#

SimpleFeature correlations#

Feature importances in linear models#

Ordinal features#

Categorical features#

Interpreting coefficients of numeric features#

Example showing how can we interpret coefficients of scaled features.#

Interim summary#

Transparency and explainability of ML models: Motivation#

Activity (~5 mins)#

Why model transparency/interpretability?#

What is model interpretability?#

Data#

Do we have class imbalance?#

Baseline#

Different models#

Feature importances in linear models#

Model interpretability beyond linear models#

sklearn’s feature_importances_ and permutation_importance#

Activity (~5 mins)#

Do we have correlated features?#

sklearn’s feature_importances_ attribute vs permutation_importance#

Decision tree feature importances#

Random forest feature importances#

Key point#

How can we get feature importances for non sklearn models?#

SHAP (SHapley Additive exPlanations) introduction#

Explaining a prediction#

SHAP (SHapley Additive exPlanations)#

Our focus#

SHAP on LGBM model#

SHAP plots#

Force plots#

Explaining a prediction#

Global feature importance using SHAP#

Dependence plot#

Summary plot#

Other tools#

Why do we want this information?#

Let’s separate `X` and `y`#

`sklearn`’s `feature_importances_` and `permutation_importance`#

`sklearn`’s `feature_importances_` attribute vs `permutation_importance`#

How can we get feature importances for non `sklearn` models?#