
Lecture 22: Communication#
UBC 2024-25
Imports#
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sys, os
sys.path.append(os.path.join(os.path.abspath(".."), "code"))
from plotting_functions import *
from sklearn.compose import ColumnTransformer, TransformedTargetRegressor
from sklearn.dummy import DummyClassifier, DummyRegressor
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.impute import SimpleImputer
from sklearn.linear_model import Ridge
from sklearn.metrics import log_loss
from sklearn.model_selection import (
GridSearchCV,
cross_val_score,
cross_validate,
train_test_split,
)
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.preprocessing import (
MinMaxScaler,
OneHotEncoder,
OrdinalEncoder,
StandardScaler,
)
DATA_DIR = os.path.join(os.path.abspath(".."), "data/")
plt.rcParams["font.size"] = 12
Learning objectives#
When communicating about applied ML, tailor an explanation to the intended audience.
Apply best practices of technical communication, such as bottom-up explanations and reader-centric writing.
Given an ML problem, analyze the decision being made and the objectives.
Avoid the pitfall of thinking about ML as coding in isolation; build the habit of relating your work to the surrounding context and stakeholders.
Maintain a healthy skepticism of
predict_probascores and their possible interpretation.Be careful and precise when communicating confidence to stakeholders in an ML project.
Identify misleading visualizations.
Recap#
What is right-censored data?
What happens when we treat right-censored data the same as “regular” data?
Predicting churn vs. no churn
Predicting tenure
Throw away people who haven’t churned
Assume everyone churns today
Survival analysis encompasses predicting both churn and tenure and deals with censoring and can make rich and interesting predictions!
We can get survival curves which show the probability of survival over time.
KM model \(\rightarrow\) doesn’t look at features
CPH model \(\rightarrow\) like linear regression, does look at the features and provides coefficients associated with each feature
Attribution#
The first part of this lecture is adapted from DSCI 542, created by David Laing.
The visualization component of this lecture benefited from discussions with DSCI 531 instructors.
Motivation#
Why should we care about effective communication?#
Most ML practitioners work in an organization with >1 people.
There will very likely be stakeholders other than yourself.
Some of them might not have any background in ML or computer science.
If your ML model is going to automate some important decisions in the organization you need to be able to explain
What does a particular result mean?
When does the model work?
What are the risks? When does it fail?
Why the model made a certain prediction for a particular example?
What are the consequences of using your model?
If you are able to convince your manager that using is model is beneficial, then only there are chances of your work going in production.
That said, you want to be honest when discussing the aspects above. If you mis-communicate the performance of your model, people will find out when the deployed model does not quite give similar performance.
Is this misleading?#

What additional information would you need to evaluate the validity of this claim?
How would you rephrase this headline to make it more accurate and less misleading?
What metrics would you use to evaluate the performance of a model like this?
Activity: explaining GridSearchCV (15 min)#
Below are two possible explanations of GridSearchCV pitched to different audiences. Read them both and then follow the instructions at the end.
Explanation 1#
Machine learning algorithms, like an airplane’s cockpit, typically involve a bunch of knobs and switches that need to be set.

For example, check out the documentation of the popular random forest algorithm here. Here’s a list of the function arguments, along with their default values (from the documentation):
class sklearn.ensemble.RandomForestClassifier(n_estimators=100, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None, ccp_alpha=0.0, max_samples=None)
Holy cow, that’s a lot of knobs and switches! As a machine learning practitioner, how am I supposed to choose n_estimators? Should I leave it at the default of 100? Or try 1000? What about criterion or class_weight for that matter? Should I trust the defaults?
Enter GridSearchCV to save the day. The general strategy here is to choose the settings that perform best on the specific task of interest. So I can’t say n_estimators=100 is better than n_estimators=1000 without knowing what problem I’m working on. For a specific problem, you usually have a numerical score that measures performance. GridSearchCV is part of the popular scikit-learn Python machine learning library. It works by searching over various settings and tells you which one worked best on your problem.
The “grid” in “grid search” comes from the fact that tries all possible combinations on a grid. For example, if you want it to consider setting n_estimators to 100, 150 or 200, and you want it to consider setting criterion to 'gini' or 'entropy', then it will search over all 6 possible combinations in a grid of 3 possible values by 2 possible values:
|
|
|
|---|---|---|
|
1 |
2 |
|
3 |
4 |
|
5 |
6 |
Here is a code sample that uses GridSearchCV to select from the 6 options we just mentioned. The problem being solved is classifying images of handwritten digits into the 10 digit categories (0-9). I chose this because the dataset is conveniently built in to scikit-learn:
# imports
from sklearn import datasets
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
# load a dataset
data = datasets.load_digits()
X = data["data"]
y = data["target"]
# set up the grid search
grid_search = GridSearchCV(
RandomForestClassifier(random_state=123),
param_grid={"n_estimators": [100, 150, 200], "criterion": ["gini", "entropy"]},
)
# run the grid search
grid_search.fit(X, y)
grid_search.best_params_
{'criterion': 'gini', 'n_estimators': 200}
As we can see from the output above, the grid search selected criterion='gini', n_estimators=100, which was one of our 6 options above (specifically Option 1).
By the way, these “knobs” we’ve been setting are called [hyperparameters](https://en.wikipedia.org/wiki/Hyperparameter_(machine_learning) and the process of setting these hyperparameters automatically is called hyperparameter optimization or hyperparameter tuning.
~400 words, not including code.
Explanation 2#
I’m also pasting it below for easy access.
~400 words, not including code.
An introduction to Grid Search#

This article will explain in simple terms what grid search is and how to implement grid search using sklearn in python.
What is grid search?#
Grid search is the process of performing hyper parameter tuning in order to determine the optimal values for a given model. This is significant as the performance of the entire model is based on the hyper parameter values specified.
Why should I use it?#
If you work with ML, you know what a nightmare it is to stipulate values for hyper parameters. There are libraries that have been implemented, such as GridSearchCV of the sklearn library, in order to automate this process and make life a little bit easier for ML enthusiasts.
How does it work?#
Here’s a python implementation of grid search using GridSearchCV of the sklearn library.
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVR
gsc = GridSearchCV(
estimator=SVR(kernel='rbf'),
param_grid={
'C': [0.1, 1, 100, 1000],
'epsilon': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 5, 10],
'gamma': [0.0001, 0.001, 0.005, 0.1, 1, 3, 5]
},
cv=5, scoring='neg_mean_squared_error', verbose=0, n_jobs=-1)
First, we need to import GridSearchCV from the sklearn library, a machine learning library for python. The estimator parameter of GridSearchCV requires the model we are using for the hyper parameter tuning process. For this example, we are using the rbf kernel of the Support Vector Regression model(SVR). The param_grid parameter requires a list of parameters and the range of values for each parameter of the specified estimator. The most significant parameters required when working with the rbf kernel of the SVR model are c, gamma and epsilon. A list of values to choose from should be given to each hyper parameter of the model. You can change these values and experiment more to see which value ranges give better performance. A cross validation process is performed in order to determine the hyper parameter value set which provides the best accuracy levels.
grid_result = gsc.fit(X, y)
best_params = grid_result.best_params_
best_svr = SVR(kernel='rbf', C=best_params["C"], epsilon=best_params["epsilon"], gamma=best_params["gamma"],
coef0=0.1, shrinking=True,
tol=0.001, cache_size=200, verbose=False, max_iter=-1)
We then use the best set of hyper parameter values chosen in the grid search, in the actual model as shown above.
If you want to know how to use grid search and cross-validation and train and test a model check out this article.
Hope this article helped you. Until next time…Adios!
Discussion questions:#
What do you like about each explanation?
What do you dislike about each explanation?
What do you think is the intended audience for each explanation?
Which explanation do you think is more effective overall for someone on Day 1 of CPSC 330?
Each explanation has an image. Which one is more effective? What are the pros/cons?
Each explanation has some sample code. Which one is more effective? What are the pros/cons?
After you’re done reading, take ~5 min to consider the discussion questions above. Paste your answer to at least one of the above questions in this Google document.
Principles of good explanations (~15 min)#
Concepts then labels, not the other way around#
The first explanation start with an analogy for the concept (and the label is left until the very end):
Machine learning algorithms, like an airplane’s cockpit, typically involve a bunch of knobs and switches that need to be set.
In the second explanation, the first sentence is wasted on anyone who doesn’t already know what “hyperparameter tuning” means:
Grid search is the process of performing hyper parameter tuning in order to determine the optimal values for a given model.
The effectiveness of these different statements depend on your audience.
See this video:
I learned very early the difference between knowing the name of something and knowing something.” - Richard Feynman.
Bottom-up explanations#
The Curse of Knowledge leads to top-down explanations:
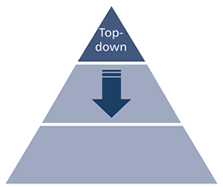
When you know something well, you think about things in the context of all your knowledge.
Those lacking the context, or frame of mind, cannot easily understand.
There is another way: bottom-up explanations:
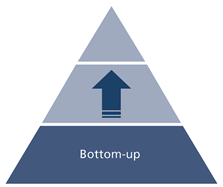
When you’re brand new to a concept, you benefit from analogies, concrete examples and familiar patterns.
In the previous examples, which one represented a bottom-up explanation and which one a top-down explanation?
New ideas in small chunks#
The first explanation has a hidden conceptual skeleton:
The concept of setting a bunch of values.
Random forest example.
The problem / pain point.
The solution.
How it works - high level.
How it works - written example.
How it works - code example.
The name of what we were discussing all this time.
Reuse your running examples#
Effective explanations often use the same example throughout the text and code. This helps readers follow the line of reasoning.
Approach from all angles#
When we’re trying to draw mental boundaries around a concept, it’s helpful to see examples on all sides of those boundaries. If we were writing a longer explanation, it might have been better to show more, e.g.
Performance with and without hyperparameter tuning.
Other types of hyperparameter tuning (e.g.
RandomizedSearchCV).
When experimenting, show the results asap#
The first explanation shows the output of the code, whereas the second does not. This is easy to do and makes a big difference.
Interesting to you != useful to the reader (aka it’s not about you)#
Here is something which was deleted from the explanation:
Some hyperparameters, like
n_estimatorsare numeric. Numeric hyperparameters are like the knobs in the cockpit: you can tune them continuously.n_estimatorsis numeric. Categorical hyperparameters are like the switches in the cockpit: they can take on (two or more) distinct values.criterionis categorical.
It’s a very elegant analogy! But is it helpful?
And furthermore, what is my hidden motivation for wanting to include it? Elegance, art, and the pursuit of higher beauty? Or making myself look smart? So maybe another name for this principle could be It’s not about you.
ML and decision-making (5 min)#
❓❓ Questions for you#
Imagine you are tasked with developing a recommender system for YouTube. You possess data on which users clicked on which videos. After spending considerable time building a recommender system using this data, you realize it isn’t producing high-quality recommendations. What could be the reasons for this?
Think beyond the data that’s given to you. Questions you have to consider:
Who is the decision maker?
What are their objectives?
What are their alternatives?
What is their context?
What data do I need?
There is often a wide gap between what people care about and what ML can do.
To understand what ML can do, let’s think about what decisions will be made using ML.
Decisions involve a few key pieces#
The decision variable: the variable that is manipulated through the decision.
E.g. how much should I sell my house for? (numeric)
E.g. should I sell my house? (categorical)
The decision-maker’s objectives: the variables that the decision-maker ultimately cares about, and wishes to manipulate indirectly through the decision variable.
E.g. my total profit, time to sale, etc.
The context: the variables that mediate the relationship between the decision variable and the objectives.
E.g. the housing market, cost of marketing it, my timeline, etc.
Break (5 min)#

Confidence and predict_proba (20 min)#
What does it mean to be “confident” in your results?
When you perform analysis, you are responsible for many judgment calls.
As you make these judgments and start to form conclusions, how can you recognize your own uncertainties about the data so that you can communicate confidently?
What does this mean for us, when we’re trying to make claims about our data?#
Let’s imagine that the following claim is true:
Vancouver has the highest cost of living of all cities in Canada.
Now let’s consider a few beliefs we could hold:
Vancouver has the highest cost of living of all cities in Canada. I am 95% sure of this.
Vancouver has the highest cost of living of all cities in Canada. I am 55% sure of this.
The part is bold is called a credence. Which belief is better?
But what if it’s actually Toronto that has the highest cost of living in Canada?
Vancouver has the highest cost of living of all cities in Canada. I am 95% sure of this.
Vancouver has the highest cost of living of all cities in Canada. I am 55% sure of this.
Which belief is better now?
Conclusion: We don’t just want to be right. We want to be confident when we’re right and hesitant when we’re wrong.
❓❓ Questions for you#
In our final exam, imagine if, along with your answers, we ask you to also provide a confidence score for each. This would involve rating how sure you are about each answer, perhaps on a percentage scale from 0% (completely unsure) to 100% (completely sure). This method not only assesses your knowledge but also your awareness of your own understanding, potentially impacting the grading process and highlighting areas for improvement. Who supports this idea 😉?
What does this have to do with applied ML?#
What if you
predictthat a credit card transaction is fraudulent?We probably want
predict_probaa lot of the time.
What if
predict_probais 0.95 in that case?How confident are YOU?
What if you forecast that avocado prices will go up next week?
How confident are you there?
Or what if you predict a house price to be \$800k?
That is not even a true/false statement.
Preferences in LogisticRegression#
When you call fit for LogisticRegression it has similar preferences:
correct and confident
> correct and hesitant
> incorrect and hesitant
> incorrect and confident
This is a “loss” or “error” function like mean squared error, so lower values are better.
When you call
fitit tries to minimize this metric.
What should be the loss? (Activity: 4 mins)#
Consider the following made-up classification example where target (true
y) is binary: -1 or 1.The true \(y\) (
y_true) and models raw scores (\(w^Tx_i\)) are given to you.You want to figure out how do you want to punish the mistakes made by the current model.
How will you punish the model in each case?
data = {
"y_true": [1, 1, 1, 1, -1, -1, -1, -1],
"raw score ($w^Tx_i$)": [10.0, 0.51, -0.1, -10, -12.0, -1.0, 0.4, 18.0],
"correct? (yes/no)":["yes", "yes", "no", "no", "yes", "yes", "no", "no"],
"confident/hesitant?":["confident", "hesitant", "hesitant", "confident", "confident", "hesistant", "hesitant", "confident"],
"punishment":["None", "small punishment", "", "", "", "", "", ""]
}
pd.DataFrame(data)
| y_true | raw score ($w^Tx_i$) | correct? (yes/no) | confident/hesitant? | punishment | |
|---|---|---|---|---|---|
| 0 | 1 | 10.00 | yes | confident | None |
| 1 | 1 | 0.51 | yes | hesitant | small punishment |
| 2 | 1 | -0.10 | no | hesitant | |
| 3 | 1 | -10.00 | no | confident | |
| 4 | -1 | -12.00 | yes | confident | |
| 5 | -1 | -1.00 | yes | hesistant | |
| 6 | -1 | 0.40 | no | hesitant | |
| 7 | -1 | 18.00 | no | confident |
grid = np.linspace(-2, 2, 1000)
plot_loss_diagram()
plt.plot(grid, np.log(1 + np.exp(-grid)), color="green", linewidth=2, label="logistic")
plt.legend(loc="best", fontsize=12);
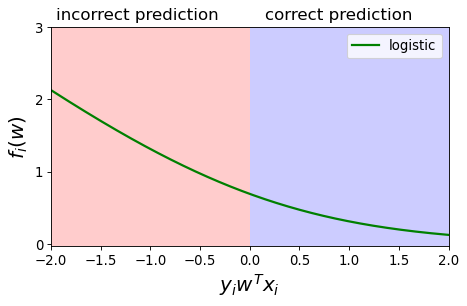
When you are confident and correct, the loss is much smaller
When you are hesitant and correct, the loss is a bit higher
If you are hesitant and incorrect the loss is even higher
If you are confident and incorrect the loss is quite high.
Your loss goes to 0 as you approach 100% confidence in the correct answer.
Your loss goes to infinity as you approach 100% confidence in the incorrect answer.
The above picture shows loss for one example.
The real
LogisticRegressiontakes summations of losses over all examples.
Some nice examples:
(Optional) See also the very related How to assign partial credit on an exam of true-false questions?
-
Look at how the plot starts at 50%. That is because being 40% confident of “X” is the same as being 60% confident of “not X”.
Visualizing your results#
Very powerful but at the same time can be misleading if not done properly.
Pre-viewing review from Calling BS visualization videos:
Dataviz in the popular media.
e.g. modern NYT
Misleading axes.
e.g. vaccines
Manipulating bin sizes.
e.g. tax dollars
Dataviz ducks.
e.g. drinking water
“look how clever we are about design” -> making it about me instead of about you (see last class)
Glass slippers.
The principle of proportional ink.
e.g. most read books
Principle of proportional ink from a viz textbook.
Dataset#
We’ll be using Kaggle House Prices dataset, which we used in lecture 10. As usual, to run this notebook you’ll need to download the data. For this dataset, train and test have already been separated. We’ll be working with the train portion.
df = pd.read_csv(DATA_DIR + "housing-kaggle/train.csv")
train_df, test_df = train_test_split(df, test_size=0.10, random_state=123)
train_df.head()
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 302 | 303 | 20 | RL | 118.0 | 13704 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 1 | 2006 | WD | Normal | 205000 |
| 767 | 768 | 50 | RL | 75.0 | 12508 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | Shed | 1300 | 7 | 2008 | WD | Normal | 160000 |
| 429 | 430 | 20 | RL | 130.0 | 11457 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 3 | 2009 | WD | Normal | 175000 |
| 1139 | 1140 | 30 | RL | 98.0 | 8731 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2007 | WD | Normal | 144000 |
| 558 | 559 | 60 | RL | 57.0 | 21872 | Pave | NaN | IR2 | HLS | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 8 | 2008 | WD | Normal | 175000 |
5 rows × 81 columns
train_df.shape
(1314, 81)
Let’s separate X and y#
X_train = train_df.drop(columns=["SalePrice"])
y_train = train_df["SalePrice"]
X_test = test_df.drop(columns=["SalePrice"])
y_test = test_df["SalePrice"]
Feature types#
We have mixed feature types and a bunch of missing values.
Now, let’s identify feature types and transformations.
drop_features = ["Id"]
numeric_features = [
"BedroomAbvGr",
"KitchenAbvGr",
"LotFrontage",
"LotArea",
"OverallQual",
"OverallCond",
"YearBuilt",
"YearRemodAdd",
"MasVnrArea",
"BsmtFinSF1",
"BsmtFinSF2",
"BsmtUnfSF",
"TotalBsmtSF",
"1stFlrSF",
"2ndFlrSF",
"LowQualFinSF",
"GrLivArea",
"BsmtFullBath",
"BsmtHalfBath",
"FullBath",
"HalfBath",
"TotRmsAbvGrd",
"Fireplaces",
"GarageYrBlt",
"GarageCars",
"GarageArea",
"WoodDeckSF",
"OpenPorchSF",
"EnclosedPorch",
"3SsnPorch",
"ScreenPorch",
"PoolArea",
"MiscVal",
"YrSold",
]
ordinal_features_reg = [
"ExterQual",
"ExterCond",
"BsmtQual",
"BsmtCond",
"HeatingQC",
"KitchenQual",
"FireplaceQu",
"GarageQual",
"GarageCond",
"PoolQC",
]
ordering = [
"Po",
"Fa",
"TA",
"Gd",
"Ex",
] # if N/A it will just impute something, per below
ordering_ordinal_reg = [ordering] * len(ordinal_features_reg)
ordering_ordinal_reg
[['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex']]
ordinal_features_oth = [
"BsmtExposure",
"BsmtFinType1",
"BsmtFinType2",
"Functional",
"Fence",
]
ordering_ordinal_oth = [
["NA", "No", "Mn", "Av", "Gd"],
["NA", "Unf", "LwQ", "Rec", "BLQ", "ALQ", "GLQ"],
["NA", "Unf", "LwQ", "Rec", "BLQ", "ALQ", "GLQ"],
["Sal", "Sev", "Maj2", "Maj1", "Mod", "Min2", "Min1", "Typ"],
["NA", "MnWw", "GdWo", "MnPrv", "GdPrv"],
]
The remaining features are categorical features.
categorical_features = list(
set(X_train.columns)
- set(numeric_features)
- set(ordinal_features_reg)
- set(ordinal_features_oth)
- set(drop_features)
)
categorical_features
['MoSold',
'PavedDrive',
'Foundation',
'RoofStyle',
'GarageFinish',
'Electrical',
'Exterior1st',
'MasVnrType',
'LotConfig',
'SaleCondition',
'SaleType',
'Neighborhood',
'HouseStyle',
'Alley',
'LandSlope',
'Condition2',
'BldgType',
'Condition1',
'Heating',
'Utilities',
'Street',
'RoofMatl',
'MiscFeature',
'GarageType',
'LandContour',
'CentralAir',
'MSSubClass',
'MSZoning',
'Exterior2nd',
'LotShape']
Applying feature transformations#
Since we have mixed feature types, let’s use
ColumnTransformerto apply different transformations on different features types.
from sklearn.compose import ColumnTransformer, make_column_transformer
numeric_transformer = make_pipeline(SimpleImputer(strategy="median"), StandardScaler())
ordinal_transformer_reg = make_pipeline(
SimpleImputer(strategy="most_frequent"),
OrdinalEncoder(categories=ordering_ordinal_reg),
)
ordinal_transformer_oth = make_pipeline(
SimpleImputer(strategy="most_frequent"),
OrdinalEncoder(categories=ordering_ordinal_oth),
)
categorical_transformer = make_pipeline(
SimpleImputer(strategy="constant", fill_value="missing"),
OneHotEncoder(handle_unknown="ignore", sparse_output=False),
)
preprocessor = make_column_transformer(
("drop", drop_features),
(numeric_transformer, numeric_features),
(ordinal_transformer_reg, ordinal_features_reg),
(ordinal_transformer_oth, ordinal_features_oth),
(categorical_transformer, categorical_features),
)
Examining the preprocessed data#
preprocessor.fit(X_train)
# Calling fit to examine all the transformers.
ColumnTransformer(transformers=[('drop', 'drop', ['Id']),
('pipeline-1',
Pipeline(steps=[('simpleimputer',
SimpleImputer(strategy='median')),
('standardscaler',
StandardScaler())]),
['BedroomAbvGr', 'KitchenAbvGr', 'LotFrontage',
'LotArea', 'OverallQual', 'OverallCond',
'YearBuilt', 'YearRemodAdd', 'MasVnrArea',
'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF',
'TotalBsmtSF', '...
['MoSold', 'PavedDrive', 'Foundation',
'RoofStyle', 'GarageFinish', 'Electrical',
'Exterior1st', 'MasVnrType', 'LotConfig',
'SaleCondition', 'SaleType', 'Neighborhood',
'HouseStyle', 'Alley', 'LandSlope',
'Condition2', 'BldgType', 'Condition1',
'Heating', 'Utilities', 'Street', 'RoofMatl',
'MiscFeature', 'GarageType', 'LandContour',
'CentralAir', 'MSSubClass', 'MSZoning',
'Exterior2nd', 'LotShape'])])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(transformers=[('drop', 'drop', ['Id']),
('pipeline-1',
Pipeline(steps=[('simpleimputer',
SimpleImputer(strategy='median')),
('standardscaler',
StandardScaler())]),
['BedroomAbvGr', 'KitchenAbvGr', 'LotFrontage',
'LotArea', 'OverallQual', 'OverallCond',
'YearBuilt', 'YearRemodAdd', 'MasVnrArea',
'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF',
'TotalBsmtSF', '...
['MoSold', 'PavedDrive', 'Foundation',
'RoofStyle', 'GarageFinish', 'Electrical',
'Exterior1st', 'MasVnrType', 'LotConfig',
'SaleCondition', 'SaleType', 'Neighborhood',
'HouseStyle', 'Alley', 'LandSlope',
'Condition2', 'BldgType', 'Condition1',
'Heating', 'Utilities', 'Street', 'RoofMatl',
'MiscFeature', 'GarageType', 'LandContour',
'CentralAir', 'MSSubClass', 'MSZoning',
'Exterior2nd', 'LotShape'])])['Id']
drop
['BedroomAbvGr', 'KitchenAbvGr', 'LotFrontage', 'LotArea', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd', 'MasVnrArea', 'BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath', 'TotRmsAbvGrd', 'Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF', 'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'YrSold']
SimpleImputer(strategy='median')
StandardScaler()
['ExterQual', 'ExterCond', 'BsmtQual', 'BsmtCond', 'HeatingQC', 'KitchenQual', 'FireplaceQu', 'GarageQual', 'GarageCond', 'PoolQC']
SimpleImputer(strategy='most_frequent')
OrdinalEncoder(categories=[['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex'],
['Po', 'Fa', 'TA', 'Gd', 'Ex']])['BsmtExposure', 'BsmtFinType1', 'BsmtFinType2', 'Functional', 'Fence']
SimpleImputer(strategy='most_frequent')
OrdinalEncoder(categories=[['NA', 'No', 'Mn', 'Av', 'Gd'],
['NA', 'Unf', 'LwQ', 'Rec', 'BLQ', 'ALQ', 'GLQ'],
['NA', 'Unf', 'LwQ', 'Rec', 'BLQ', 'ALQ', 'GLQ'],
['Sal', 'Sev', 'Maj2', 'Maj1', 'Mod', 'Min2', 'Min1',
'Typ'],
['NA', 'MnWw', 'GdWo', 'MnPrv', 'GdPrv']])['MoSold', 'PavedDrive', 'Foundation', 'RoofStyle', 'GarageFinish', 'Electrical', 'Exterior1st', 'MasVnrType', 'LotConfig', 'SaleCondition', 'SaleType', 'Neighborhood', 'HouseStyle', 'Alley', 'LandSlope', 'Condition2', 'BldgType', 'Condition1', 'Heating', 'Utilities', 'Street', 'RoofMatl', 'MiscFeature', 'GarageType', 'LandContour', 'CentralAir', 'MSSubClass', 'MSZoning', 'Exterior2nd', 'LotShape']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
ohe_columns = list(
preprocessor.named_transformers_["pipeline-4"]
.named_steps["onehotencoder"]
.get_feature_names_out(categorical_features)
)
new_columns = (
numeric_features + ordinal_features_reg + ordinal_features_oth + ohe_columns
)
X_train_enc = pd.DataFrame(
preprocessor.transform(X_train), index=X_train.index, columns=new_columns
)
X_train_enc.head()
| BedroomAbvGr | KitchenAbvGr | LotFrontage | LotArea | OverallQual | OverallCond | YearBuilt | YearRemodAdd | MasVnrArea | BsmtFinSF1 | ... | Exterior2nd_Plywood | Exterior2nd_Stone | Exterior2nd_Stucco | Exterior2nd_VinylSd | Exterior2nd_Wd Sdng | Exterior2nd_Wd Shng | LotShape_IR1 | LotShape_IR2 | LotShape_IR3 | LotShape_Reg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 302 | 0.154795 | -0.222647 | 2.312501 | 0.381428 | 0.663680 | -0.512408 | 0.993969 | 0.840492 | 0.269972 | -0.961498 | ... | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 767 | 1.372763 | -0.222647 | 0.260890 | 0.248457 | -0.054669 | 1.285467 | -1.026793 | 0.016525 | -0.573129 | 0.476092 | ... | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 429 | 0.154795 | -0.222647 | 2.885044 | 0.131607 | -0.054669 | -0.512408 | 0.563314 | 0.161931 | -0.573129 | 1.227559 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 1139 | 0.154795 | -0.222647 | 1.358264 | -0.171468 | -0.773017 | -0.512408 | -1.689338 | -1.679877 | -0.573129 | 0.443419 | ... | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 558 | 0.154795 | -0.222647 | -0.597924 | 1.289541 | 0.663680 | -0.512408 | 0.828332 | 0.598149 | -0.573129 | 0.354114 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
5 rows × 262 columns
X_test_enc = pd.DataFrame(
preprocessor.transform(X_test), index=X_test.index, columns=new_columns
)
X_test_enc.head()
| BedroomAbvGr | KitchenAbvGr | LotFrontage | LotArea | OverallQual | OverallCond | YearBuilt | YearRemodAdd | MasVnrArea | BsmtFinSF1 | ... | Exterior2nd_Plywood | Exterior2nd_Stone | Exterior2nd_Stucco | Exterior2nd_VinylSd | Exterior2nd_Wd Sdng | Exterior2nd_Wd Shng | LotShape_IR1 | LotShape_IR2 | LotShape_IR3 | LotShape_Reg | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 147 | 0.154795 | -0.222647 | -0.025381 | -0.085415 | 0.663680 | -0.512408 | 0.993969 | 0.792023 | 0.438592 | -0.961498 | ... | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| 676 | 1.372763 | 4.348569 | -0.454788 | -0.074853 | -1.491366 | -3.209221 | -2.351883 | -1.679877 | -0.573129 | -0.961498 | ... | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 1304 | 0.154795 | -0.222647 | -1.790721 | -0.768279 | 0.663680 | -0.512408 | 1.093350 | 0.937429 | 0.084490 | -0.961498 | ... | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 1372 | 0.154795 | -0.222647 | 0.260890 | -0.058176 | 0.663680 | 0.386530 | 0.894587 | 0.646617 | -0.573129 | 1.162214 | ... | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 1427 | 0.154795 | -0.222647 | -0.454788 | 0.073016 | -0.773017 | 0.386530 | -0.861157 | -1.679877 | -0.573129 | 0.301838 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
5 rows × 262 columns
X_train.shape, X_test.shape
((1314, 80), (146, 80))
Training random forests and gradient boosted trees#
from sklearn.ensemble import GradientBoostingRegressor
Let’s compare sklearn’s GradientBoostingRegressor to RandomForestRegressor for different values of n_estimators.
n_estimators_values = [3, 10, 30, 100, 300]
score_rf_train = list()
score_rf_test = list()
score_gb_train = list()
score_gb_test = list()
for n_estimators in n_estimators_values:
print(n_estimators)
rf = TransformedTargetRegressor(
RandomForestRegressor(n_estimators=n_estimators, random_state=123),
func=np.log1p,
inverse_func=np.expm1,
)
rf.fit(X_train_enc, y_train)
score_rf_train.append(rf.score(X_train_enc, y_train))
score_rf_test.append(rf.score(X_test_enc, y_test))
gb = TransformedTargetRegressor(
GradientBoostingRegressor(n_estimators=n_estimators, random_state=123),
func=np.log1p,
inverse_func=np.expm1,
)
gb.fit(X_train_enc, y_train)
score_gb_train.append(gb.score(X_train_enc, y_train))
score_gb_test.append(gb.score(X_test_enc, y_test))
3
10
30
100
300
Confusing and perhaps misleading visualization of results#
Here is a low-quality plot that is confusing and perhaps downright misleading:
plt.figure(figsize=(6,6));
plt.subplot(2, 1, 1)
plt.plot(n_estimators_values, score_rf_train, label="rf train")
plt.plot(n_estimators_values, score_rf_test, label="rf test")
plt.ylabel("$R^2$ score")
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(n_estimators_values, score_gb_train, label="gb train")
plt.plot(n_estimators_values, score_gb_test, label="gb test")
plt.xlabel("n estimators")
plt.ylabel("$R^2$ score")
plt.legend()
plt.tight_layout();
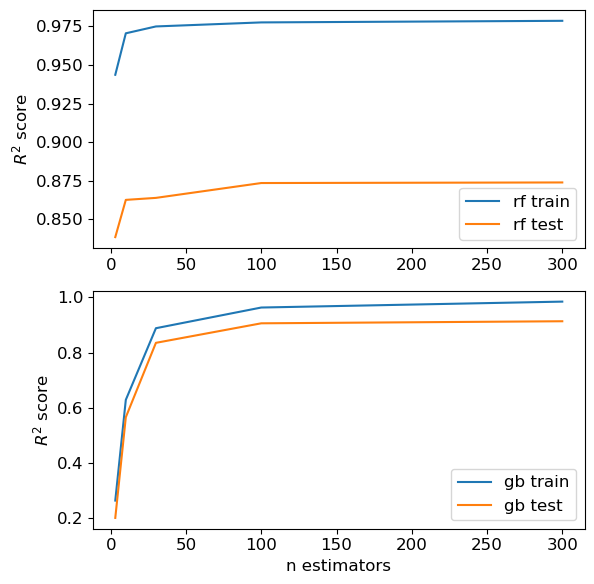
Could you create some visualizations such that it makes
RF look better than GB
GB look better than RF
RF and GB look equally good
You can create your own misleading example and copy or screenshot it and paste it into this Google document.
Here are some misleading plots.
RF better than GB#
plt.figure(figsize=(6,4))
nmax = 3
# plt.plot(n_estimators_values[:nmax], score_rf_train[:nmax], label="rf train")
plt.plot(n_estimators_values[:nmax], score_rf_test[:nmax], label="rf test")
# plt.plot(n_estimators_values[:nmax], score_gb_train[:nmax], label="gb train")
plt.plot(n_estimators_values[:nmax], score_gb_test[:nmax], label="gb test")
plt.xlabel("n estimators")
plt.ylabel("$R^2$ score")
plt.legend()
plt.title("for most values of n_estimators, RF is betteR!!");
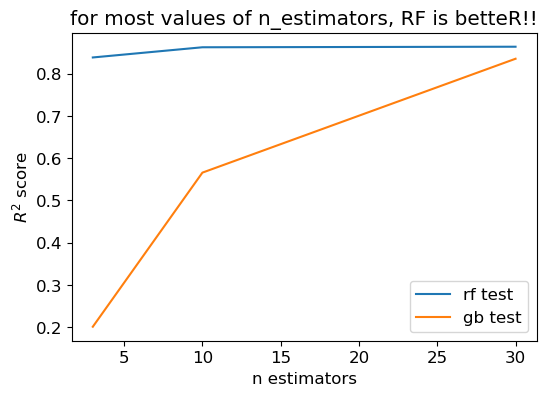
GB better than RF#
plt.plot(n_estimators_values, score_rf_test, label="rf test")
plt.plot(n_estimators_values, score_gb_test, label="gb test")
plt.xlabel("n estimators")
plt.ylabel("$R^2$ score")
plt.legend()
plt.title("GB better!!!");
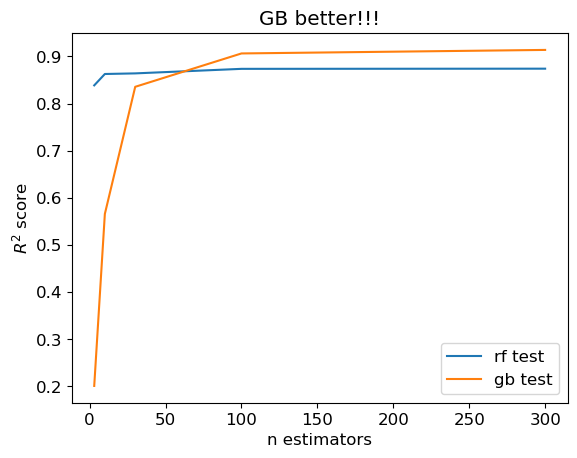
Equally good#
nmax = 4
# plt.plot(n_estimators_values, score_rf_train, label="rf train")
plt.plot(n_estimators_values[:nmax], score_rf_test[:nmax], "b", label="rf test")
plt.ylabel("RF $R^2$ score")
plt.ylim((-10, 1.2))
plt.legend(loc=0)
plt.twinx()
# plt.plot(n_estimators_values, score_gb_train, label="gb train")
plt.plot(n_estimators_values[:nmax], score_gb_test[:nmax], "--r", label="gb test")
plt.legend(loc=4)
plt.xlabel("n estimators")
plt.ylabel("GB $R^2$ score")
plt.ylim((-10, 1.25))
#plt.ylim((-0.01, 0.70))
plt.title("Both equally good!!!");
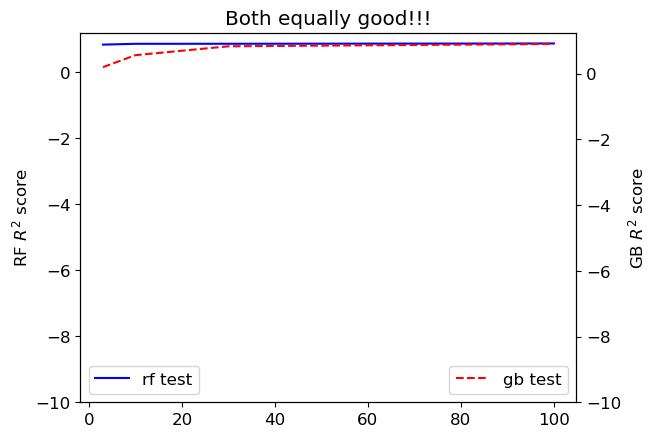
Things to watch out for#
Chopping off the x-axis
the practice of starting the x-axis (or sometimes the y-axis) at a value other than zero to exaggerate the changes in the data
Saturate the axes
where the axes are set to ranges that are too narrow or too wide for the data being presented making it difficult to identify patterns
Bar chart for a cherry-picked values
Different y-axes
Be critical of your visualizations and try to make them as honest as possible.
What did we learn today?#
Principles of effective communication#
Concepts then labels, not the other way around
Bottom-up explanations
New ideas in small chunks
Reuse your running examples
Approaches from all angles
When experimenting, show the results asap
It’s not about you.
Decision variables, objectives, and context.
How does ML fit in?
Expressing your confidence about the results
Misleading visualizations.
Have a great weekend!

