
Lecture 5: Preprocessing and sklearn pipelines#
UBC 2024-25
Imports, LOs#
Imports#
import os
import sys
import time
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pandas as pd
from IPython.display import HTML
sys.path.append(os.path.join(os.path.abspath(".."), "code"))
import mglearn
from IPython.display import display
from plotting_functions import *
# Classifiers and regressors
from sklearn.dummy import DummyClassifier, DummyRegressor
# Preprocessing and pipeline
from sklearn.impute import SimpleImputer
# train test split and cross validation
from sklearn.model_selection import cross_val_score, cross_validate, train_test_split
from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import (
MinMaxScaler,
OneHotEncoder,
OrdinalEncoder,
StandardScaler,
)
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from utils import *
%matplotlib inline
pd.set_option("display.max_colwidth", 200)
DATA_DIR = "../data/"
Learning outcomes#
From this lecture, you will be able to
explain motivation for preprocessing in supervised machine learning;
identify when to implement feature transformations such as imputation, scaling, and one-hot encoding in a machine learning model development pipeline;
use
sklearntransformers for applying feature transformations on your dataset;discuss golden rule in the context of feature transformations;
use
sklearn.pipeline.Pipelineandsklearn.pipeline.make_pipelineto build a preliminary machine learning pipeline.
❓❓ Questions for you#
(iClicker) Exercise 5.1#
iClicker cloud join link: https://join.iclicker.com/VYFJ
Take a guess: In your machine learning project, how much time will you typically spend on data preparation and transformation?
(A) ~80% of the project time
(B) ~20% of the project time
(C) ~50% of the project time
(D) None. Most of the time will be spent on model building
The question is adapted from here.
Motivation and big picture [video]#
So far we have seen
Three ML models (decision trees, \(k\)-NNs, SVMs with RBF kernel)
ML fundamentals (train-validation-test split, cross-validation, the fundamental tradeoff, the golden rule)
Are we ready to do machine learning on real-world datasets?
Very often real-world datasets need preprocessing before we use them to build ML models.
Example: \(k\)-nearest neighbours on the Spotify dataset#
In HW2 you used
DecisionTreeClassifierto predict whether the user would like a particular song or not.Can we use \(k\)-NN classifier for this task?
Intuition: To predict whether the user likes a particular song or not (query point)
find the songs that are closest to the query point
let them vote on the target
take the majority vote as the target for the query point
In order to run the code below, you need to download the dataset from Kaggle.
spotify_df = pd.read_csv(DATA_DIR + "spotify.csv", index_col=0)
train_df, test_df = train_test_split(spotify_df, test_size=0.20, random_state=123)
X_train, y_train = (
train_df.drop(columns=["song_title", "artist", "target"]),
train_df["target"],
)
X_test, y_test = (
test_df.drop(columns=["song_title", "artist", "target"]),
test_df["target"],
)
dummy = DummyClassifier(strategy="most_frequent")
scores = cross_validate(dummy, X_train, y_train, return_train_score=True)
print("Mean validation score %0.3f" % (np.mean(scores["test_score"])))
pd.DataFrame(scores)
Mean validation score 0.508
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| 0 | 0.000452 | 0.000260 | 0.507740 | 0.507752 |
| 1 | 0.000259 | 0.000195 | 0.507740 | 0.507752 |
| 2 | 0.000240 | 0.000188 | 0.507740 | 0.507752 |
| 3 | 0.000231 | 0.000180 | 0.506211 | 0.508133 |
| 4 | 0.000235 | 0.000177 | 0.509317 | 0.507359 |
knn = KNeighborsClassifier()
scores = cross_validate(knn, X_train, y_train, return_train_score=True)
print("Mean validation score %0.3f" % (np.mean(scores["test_score"])))
pd.DataFrame(scores)
Mean validation score 0.546
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| 0 | 0.001043 | 0.006973 | 0.563467 | 0.717829 |
| 1 | 0.000867 | 0.005836 | 0.535604 | 0.721705 |
| 2 | 0.000774 | 0.005157 | 0.529412 | 0.708527 |
| 3 | 0.000765 | 0.005067 | 0.537267 | 0.721921 |
| 4 | 0.000748 | 0.005093 | 0.562112 | 0.711077 |
two_songs = X_train.sample(2, random_state=42)
two_songs
| acousticness | danceability | duration_ms | energy | instrumentalness | key | liveness | loudness | mode | speechiness | tempo | time_signature | valence | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 842 | 0.229000 | 0.494 | 147893 | 0.666 | 0.000057 | 9 | 0.0469 | -9.743 | 0 | 0.0351 | 140.832 | 4.0 | 0.704 |
| 654 | 0.000289 | 0.771 | 227143 | 0.949 | 0.602000 | 8 | 0.5950 | -4.712 | 1 | 0.1750 | 111.959 | 4.0 | 0.372 |
euclidean_distances(two_songs)
array([[ 0. , 79250.00543825],
[79250.00543825, 0. ]])
Let’s consider only two features: duration_ms and tempo.
two_songs_subset = two_songs[["duration_ms", "tempo"]]
two_songs_subset
| duration_ms | tempo | |
|---|---|---|
| 842 | 147893 | 140.832 |
| 654 | 227143 | 111.959 |
euclidean_distances(two_songs_subset)
array([[ 0. , 79250.00525962],
[79250.00525962, 0. ]])
Do you see any problem?
The distance is completely dominated by the the features with larger values
The features with smaller values are being ignored.
Does it matter?
Yes! Scale is based on how data was collected.
Features on a smaller scale can be highly informative and there is no good reason to ignore them.
We want our model to be robust and not sensitive to the scale.
Was this a problem for decision trees?
Scaling using scikit-learn’s StandardScaler#
We’ll use
scikit-learn’sStandardScaler, which is atransformer.Only focus on the syntax for now. We’ll talk about scaling in a bit.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() # create feature trasformer object
scaler.fit(X_train) # fitting the transformer on the train split
X_train_scaled = scaler.transform(X_train) # transforming the train split
X_test_scaled = scaler.transform(X_test) # transforming the test split
X_train # original X_train
| acousticness | danceability | duration_ms | energy | instrumentalness | key | liveness | loudness | mode | speechiness | tempo | time_signature | valence | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1505 | 0.004770 | 0.585 | 214740 | 0.614 | 0.000155 | 10 | 0.0762 | -5.594 | 0 | 0.0370 | 114.059 | 4.0 | 0.2730 |
| 813 | 0.114000 | 0.665 | 216728 | 0.513 | 0.303000 | 0 | 0.1220 | -7.314 | 1 | 0.3310 | 100.344 | 3.0 | 0.0373 |
| 615 | 0.030200 | 0.798 | 216585 | 0.481 | 0.000000 | 7 | 0.1280 | -10.488 | 1 | 0.3140 | 127.136 | 4.0 | 0.6400 |
| 319 | 0.106000 | 0.912 | 194040 | 0.317 | 0.000208 | 6 | 0.0723 | -12.719 | 0 | 0.0378 | 99.346 | 4.0 | 0.9490 |
| 320 | 0.021100 | 0.697 | 236456 | 0.905 | 0.893000 | 6 | 0.1190 | -7.787 | 0 | 0.0339 | 119.977 | 4.0 | 0.3110 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2012 | 0.001060 | 0.584 | 274404 | 0.932 | 0.002690 | 1 | 0.1290 | -3.501 | 1 | 0.3330 | 74.976 | 4.0 | 0.2110 |
| 1346 | 0.000021 | 0.535 | 203500 | 0.974 | 0.000149 | 10 | 0.2630 | -3.566 | 0 | 0.1720 | 116.956 | 4.0 | 0.4310 |
| 1406 | 0.503000 | 0.410 | 256333 | 0.648 | 0.000000 | 7 | 0.2190 | -4.469 | 1 | 0.0362 | 60.391 | 4.0 | 0.3420 |
| 1389 | 0.705000 | 0.894 | 222307 | 0.161 | 0.003300 | 4 | 0.3120 | -14.311 | 1 | 0.0880 | 104.968 | 4.0 | 0.8180 |
| 1534 | 0.623000 | 0.470 | 394920 | 0.156 | 0.187000 | 2 | 0.1040 | -17.036 | 1 | 0.0399 | 118.176 | 4.0 | 0.0591 |
1613 rows × 13 columns
Let’s examine transformed value of the energy feature in the first row.
X_train["energy"].iloc[0]
0.614
(X_train["energy"].iloc[0] - np.mean(X_train["energy"])) / X_train["energy"].std()
-0.3180174485124284
pd.DataFrame(X_train_scaled, columns=X_train.columns, index=X_train.index).head().round(
3
)
| acousticness | danceability | duration_ms | energy | instrumentalness | key | liveness | loudness | mode | speechiness | tempo | time_signature | valence | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1505 | -0.698 | -0.195 | -0.399 | -0.318 | -0.492 | 1.276 | -0.738 | 0.396 | -1.281 | -0.618 | -0.294 | 0.139 | -0.908 |
| 813 | -0.276 | 0.296 | -0.374 | -0.796 | 0.598 | -1.487 | -0.439 | -0.052 | 0.781 | 2.728 | -0.803 | -3.781 | -1.861 |
| 615 | -0.600 | 1.111 | -0.376 | -0.947 | -0.493 | 0.447 | -0.400 | -0.879 | 0.781 | 2.535 | 0.191 | 0.139 | 0.576 |
| 319 | -0.307 | 1.809 | -0.654 | -1.722 | -0.492 | 0.170 | -0.763 | -1.461 | -1.281 | -0.609 | -0.840 | 0.139 | 1.825 |
| 320 | -0.635 | 0.492 | -0.131 | 1.057 | 2.723 | 0.170 | -0.458 | -0.176 | -1.281 | -0.653 | -0.074 | 0.139 | -0.754 |
fit and transform paradigm for transformers#
sklearnusesfitandtransformparadigms for feature transformations.We
fitthe transformer on the train split and then transform the train split as well as the test split.We apply the same transformations on the test split.
sklearn API summary: estimators#
Suppose model is a classification or regression model.
model.fit(X_train, y_train)
X_train_predictions = model.predict(X_train)
X_test_predictions = model.predict(X_test)
sklearn API summary: transformers#
Suppose transformer is a transformer used to change the input representation, for example, to tackle missing values or to scales numeric features.
transformer.fit(X_train, [y_train])
X_train_transformed = transformer.transform(X_train)
X_test_transformed = transformer.transform(X_test)
You can pass
y_traininfitbut it’s usually ignored. It allows you to pass it just to be consistent with usual usage ofsklearn’sfitmethod.You can also carry out fitting and transforming in one call using
fit_transform. But be mindful to use it only on the train split and not on the test split.
Do you expect
DummyClassifierresults to change after scaling the data?Let’s check whether scaling makes any difference for \(k\)-NNs.
knn_unscaled = KNeighborsClassifier()
knn_unscaled.fit(X_train, y_train)
print("Train score: %0.3f" % (knn_unscaled.score(X_train, y_train)))
print("Test score: %0.3f" % (knn_unscaled.score(X_test, y_test)))
Train score: 0.726
Test score: 0.552
knn_scaled = KNeighborsClassifier()
knn_scaled.fit(X_train_scaled, y_train)
print("Train score: %0.3f" % (knn_scaled.score(X_train_scaled, y_train)))
print("Test score: %0.3f" % (knn_scaled.score(X_test_scaled, y_test)))
Train score: 0.798
Test score: 0.686
The scores with scaled data are better compared to the unscaled data in case of \(k\)-NNs.
I am not carrying out cross-validation here for a reason that we’ll look into soon.
Note that I am a bit sloppy here and using the test set several times for teaching purposes. But when you build an ML pipeline, please do assessment on the test set only once.
Common preprocessing techniques#
Some commonly performed feature transformation include:
Imputation: Tackling missing values
Scaling: Scaling of numeric features
One-hot encoding: Tackling categorical variables
We can have one lecture on each of them! In this lesson our goal is to getting familiar with them so that we can use them to build ML pipelines.
In the next part of this lecture, we’ll build an ML pipeline using California housing prices regression dataset. In the process, we will talk about different feature transformations and how can we apply them so that we do not violate the golden rule.
Imputation and scaling [video]#
Dataset, splitting, and baseline#
We’ll be working on California housing prices regression dataset to demonstrate these feature transformation techniques. The task is to predict median house values in Californian districts, given a number of features from these districts. If you are running the notebook on your own, you’ll have to download the data and put it in the data directory.
housing_df = pd.read_csv(DATA_DIR + "housing.csv")
train_df, test_df = train_test_split(housing_df, test_size=0.1, random_state=123)
train_df.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 6051 | -117.75 | 34.04 | 22.0 | 2948.0 | 636.0 | 2600.0 | 602.0 | 3.1250 | 113600.0 | INLAND |
| 20113 | -119.57 | 37.94 | 17.0 | 346.0 | 130.0 | 51.0 | 20.0 | 3.4861 | 137500.0 | INLAND |
| 14289 | -117.13 | 32.74 | 46.0 | 3355.0 | 768.0 | 1457.0 | 708.0 | 2.6604 | 170100.0 | NEAR OCEAN |
| 13665 | -117.31 | 34.02 | 18.0 | 1634.0 | 274.0 | 899.0 | 285.0 | 5.2139 | 129300.0 | INLAND |
| 14471 | -117.23 | 32.88 | 18.0 | 5566.0 | 1465.0 | 6303.0 | 1458.0 | 1.8580 | 205000.0 | NEAR OCEAN |
Some column values are mean/median but some are not.
Let’s add some new features to the dataset which could help predicting the target: median_house_value.
train_df = train_df.assign(
rooms_per_household=train_df["total_rooms"] / train_df["households"]
)
test_df = test_df.assign(
rooms_per_household=test_df["total_rooms"] / test_df["households"]
)
train_df = train_df.assign(
bedrooms_per_household=train_df["total_bedrooms"] / train_df["households"]
)
test_df = test_df.assign(
bedrooms_per_household=test_df["total_bedrooms"] / test_df["households"]
)
train_df = train_df.assign(
population_per_household=train_df["population"] / train_df["households"]
)
test_df = test_df.assign(
population_per_household=test_df["population"] / test_df["households"]
)
train_df.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6051 | -117.75 | 34.04 | 22.0 | 2948.0 | 636.0 | 2600.0 | 602.0 | 3.1250 | 113600.0 | INLAND | 4.897010 | 1.056478 | 4.318937 |
| 20113 | -119.57 | 37.94 | 17.0 | 346.0 | 130.0 | 51.0 | 20.0 | 3.4861 | 137500.0 | INLAND | 17.300000 | 6.500000 | 2.550000 |
| 14289 | -117.13 | 32.74 | 46.0 | 3355.0 | 768.0 | 1457.0 | 708.0 | 2.6604 | 170100.0 | NEAR OCEAN | 4.738701 | 1.084746 | 2.057910 |
| 13665 | -117.31 | 34.02 | 18.0 | 1634.0 | 274.0 | 899.0 | 285.0 | 5.2139 | 129300.0 | INLAND | 5.733333 | 0.961404 | 3.154386 |
| 14471 | -117.23 | 32.88 | 18.0 | 5566.0 | 1465.0 | 6303.0 | 1458.0 | 1.8580 | 205000.0 | NEAR OCEAN | 3.817558 | 1.004801 | 4.323045 |
Question: Should we remove
total_rooms,total_bedrooms, andpopulationcolumns?Probably because we have created
rooms_per_householdandbedrooms_per_householdandpopulation_per_householdfeatures which are more relevant for this task.
train_df = train_df.drop(columns=["population", "total_rooms", "total_bedrooms"])
test_df = test_df.drop(columns=["population", "total_rooms", "total_bedrooms"])
When is it OK to do things before splitting?#
Here it would have been OK to add new features before splitting because we are not using any global information in the data but only looking at one row at a time.
But just to be safe and to avoid accidentally breaking the golden rule, it’s better to do it after splitting.
EDA#
train_df.head()
| longitude | latitude | housing_median_age | households | median_income | median_house_value | ocean_proximity | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|---|---|
| 6051 | -117.75 | 34.04 | 22.0 | 602.0 | 3.1250 | 113600.0 | INLAND | 4.897010 | 1.056478 | 4.318937 |
| 20113 | -119.57 | 37.94 | 17.0 | 20.0 | 3.4861 | 137500.0 | INLAND | 17.300000 | 6.500000 | 2.550000 |
| 14289 | -117.13 | 32.74 | 46.0 | 708.0 | 2.6604 | 170100.0 | NEAR OCEAN | 4.738701 | 1.084746 | 2.057910 |
| 13665 | -117.31 | 34.02 | 18.0 | 285.0 | 5.2139 | 129300.0 | INLAND | 5.733333 | 0.961404 | 3.154386 |
| 14471 | -117.23 | 32.88 | 18.0 | 1458.0 | 1.8580 | 205000.0 | NEAR OCEAN | 3.817558 | 1.004801 | 4.323045 |
The feature scales are quite different.
train_df.info()
<class 'pandas.core.frame.DataFrame'>
Index: 18576 entries, 6051 to 19966
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 18576 non-null float64
1 latitude 18576 non-null float64
2 housing_median_age 18576 non-null float64
3 households 18576 non-null float64
4 median_income 18576 non-null float64
5 median_house_value 18576 non-null float64
6 ocean_proximity 18576 non-null object
7 rooms_per_household 18576 non-null float64
8 bedrooms_per_household 18391 non-null float64
9 population_per_household 18576 non-null float64
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
We have one categorical feature and all other features are numeric features.
train_df.describe()
| longitude | latitude | housing_median_age | households | median_income | median_house_value | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|---|
| count | 18576.000000 | 18576.000000 | 18576.000000 | 18576.000000 | 18576.000000 | 18576.000000 | 18576.000000 | 18391.000000 | 18576.000000 |
| mean | -119.565888 | 35.627966 | 28.622255 | 500.061100 | 3.862552 | 206292.067991 | 5.426067 | 1.097516 | 3.052349 |
| std | 1.999622 | 2.134658 | 12.588307 | 383.044313 | 1.892491 | 115083.856175 | 2.512319 | 0.486266 | 10.020873 |
| min | -124.350000 | 32.540000 | 1.000000 | 1.000000 | 0.499900 | 14999.000000 | 0.846154 | 0.333333 | 0.692308 |
| 25% | -121.790000 | 33.930000 | 18.000000 | 280.000000 | 2.560225 | 119400.000000 | 4.439360 | 1.005888 | 2.430323 |
| 50% | -118.490000 | 34.250000 | 29.000000 | 410.000000 | 3.527500 | 179300.000000 | 5.226415 | 1.048860 | 2.818868 |
| 75% | -118.010000 | 37.710000 | 37.000000 | 606.000000 | 4.736900 | 263600.000000 | 6.051620 | 1.099723 | 3.283921 |
| max | -114.310000 | 41.950000 | 52.000000 | 6082.000000 | 15.000100 | 500001.000000 | 141.909091 | 34.066667 | 1243.333333 |
Seems like total_bedrooms column has some missing values.
This must have affected our new feature
bedrooms_per_householdas well.
housing_df["total_bedrooms"].isnull().sum()
207
## (optional)
train_df.hist(bins=50, figsize=(20, 15));
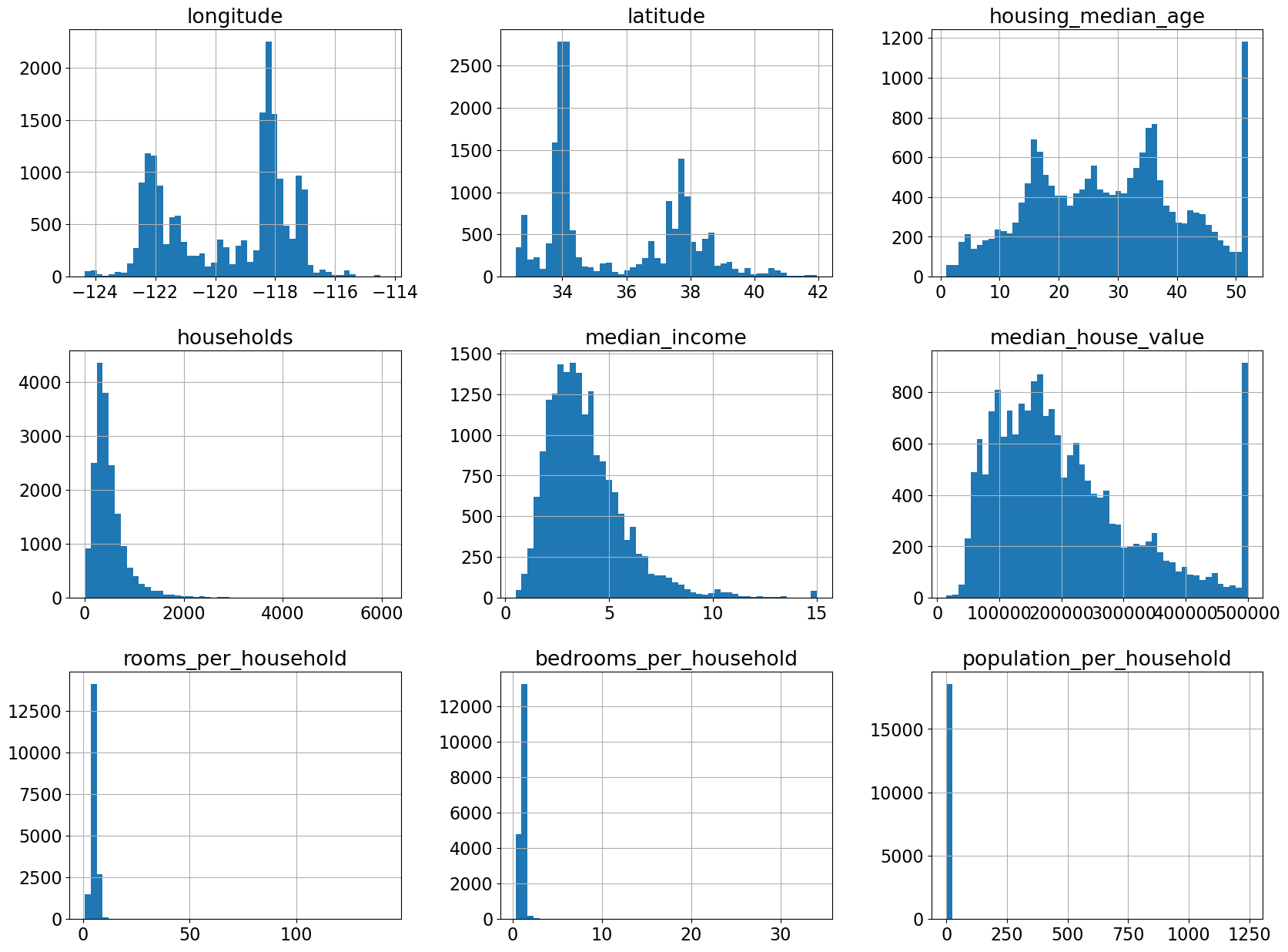
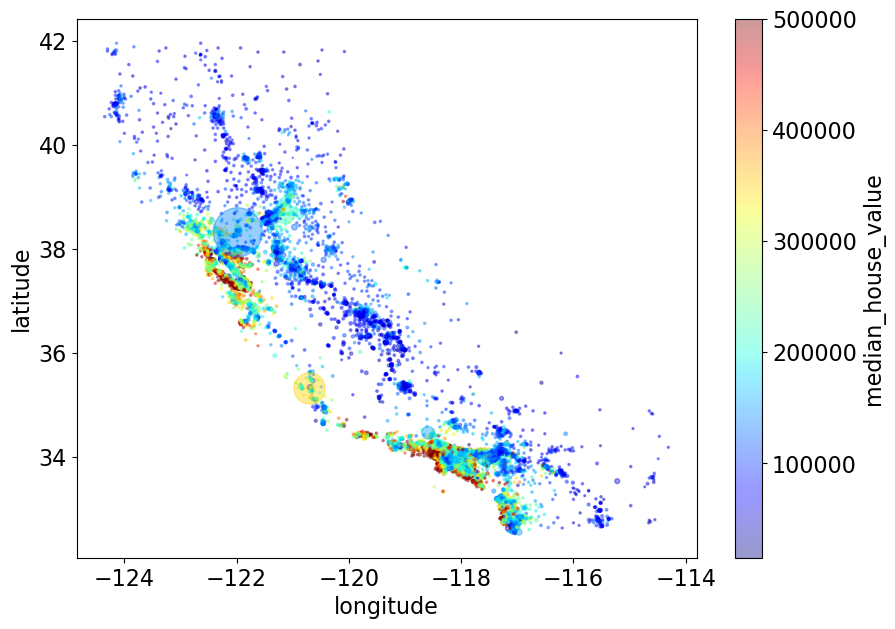
## (optional)
train_df.plot(
kind="scatter",
x="longitude",
y="latitude",
alpha=0.4,
s=train_df["population_per_household"],
figsize=(10, 7),
c="median_house_value",
cmap=plt.get_cmap("jet"),
colorbar=True,
sharex=False,
);
What all transformations we need to apply on the dataset?#
Here is what we see from the EDA.
Some missing values in
total_bedroomscolumnScales are quite different across columns.
Categorical variable
ocean_proximity
Read about preprocessing techniques implemented in scikit-learn.
# We are droping the categorical variable ocean_proximity for now. We'll come back to it in a bit.
X_train = train_df.drop(columns=["median_house_value", "ocean_proximity"])
y_train = train_df["median_house_value"]
X_test = test_df.drop(columns=["median_house_value", "ocean_proximity"])
y_test = test_df["median_house_value"]
Let’s first run our baseline model DummyRegressor#
results_dict = {} # dictionary to store our results for different models
def mean_std_cross_val_scores(model, X_train, y_train, **kwargs):
"""
Returns mean and std of cross validation
Parameters
----------
model :
scikit-learn model
X_train : numpy array or pandas DataFrame
X in the training data
y_train :
y in the training data
Returns
----------
pandas Series with mean scores from cross_validation
"""
scores = cross_validate(model, X_train, y_train, **kwargs)
mean_scores = pd.DataFrame(scores).mean()
std_scores = pd.DataFrame(scores).std()
out_col = []
for i in range(len(mean_scores)):
out_col.append((f"%0.3f (+/- %0.3f)" % (mean_scores[i], std_scores[i])))
return pd.Series(data=out_col, index=mean_scores.index)
dummy = DummyRegressor(strategy="median")
results_dict["dummy"] = mean_std_cross_val_scores(
dummy, X_train, y_train, return_train_score=True
)
/var/folders/b3/g26r0dcx4b35vf3nk31216hc0000gr/T/ipykernel_32469/4158382658.py:26: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
out_col.append((f"%0.3f (+/- %0.3f)" % (mean_scores[i], std_scores[i])))
pd.DataFrame(results_dict)
| dummy | |
|---|---|
| fit_time | 0.001 (+/- 0.000) |
| score_time | 0.000 (+/- 0.000) |
| test_score | -0.055 (+/- 0.012) |
| train_score | -0.055 (+/- 0.001) |
Imputation#
X_train
| longitude | latitude | housing_median_age | households | median_income | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|
| 6051 | -117.75 | 34.04 | 22.0 | 602.0 | 3.1250 | 4.897010 | 1.056478 | 4.318937 |
| 20113 | -119.57 | 37.94 | 17.0 | 20.0 | 3.4861 | 17.300000 | 6.500000 | 2.550000 |
| 14289 | -117.13 | 32.74 | 46.0 | 708.0 | 2.6604 | 4.738701 | 1.084746 | 2.057910 |
| 13665 | -117.31 | 34.02 | 18.0 | 285.0 | 5.2139 | 5.733333 | 0.961404 | 3.154386 |
| 14471 | -117.23 | 32.88 | 18.0 | 1458.0 | 1.8580 | 3.817558 | 1.004801 | 4.323045 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 7763 | -118.10 | 33.91 | 36.0 | 130.0 | 3.6389 | 5.584615 | NaN | 3.769231 |
| 15377 | -117.24 | 33.37 | 14.0 | 779.0 | 4.5391 | 6.016688 | 1.017972 | 3.127086 |
| 17730 | -121.76 | 37.33 | 5.0 | 697.0 | 5.6306 | 5.958393 | 1.031564 | 3.493544 |
| 15725 | -122.44 | 37.78 | 44.0 | 326.0 | 3.8750 | 4.739264 | 1.024540 | 1.720859 |
| 19966 | -119.08 | 36.21 | 20.0 | 348.0 | 2.5156 | 5.491379 | 1.117816 | 3.566092 |
18576 rows × 8 columns
knn = KNeighborsRegressor()
# knn.fit(X_train, y_train)
What’s the problem?#
ValueError: Input X contains NaN.
The classifier is not able to deal with missing values (NaNs).
What are possible ways to deal with the problem?
Delete the rows?
Replace them with some reasonable values?
SimpleImputeris a transformer insklearnto deal with this problem. For example,You can impute missing values in categorical columns with the most frequent value.
You can impute the missing values in numeric columns with the mean or median of the column.
X_train.sort_values("bedrooms_per_household")
| longitude | latitude | housing_median_age | households | median_income | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|
| 20248 | -119.23 | 34.25 | 28.0 | 9.0 | 8.0000 | 2.888889 | 0.333333 | 3.222222 |
| 12649 | -121.47 | 38.51 | 52.0 | 9.0 | 3.6250 | 2.222222 | 0.444444 | 8.222222 |
| 3125 | -117.76 | 35.22 | 4.0 | 6.0 | 1.6250 | 3.000000 | 0.500000 | 1.333333 |
| 12138 | -117.22 | 33.87 | 16.0 | 14.0 | 2.6250 | 4.000000 | 0.500000 | 2.785714 |
| 8219 | -118.21 | 33.79 | 33.0 | 36.0 | 4.5938 | 0.888889 | 0.500000 | 2.666667 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 4591 | -118.28 | 34.06 | 42.0 | 1179.0 | 1.2254 | 2.096692 | NaN | 3.218830 |
| 19485 | -120.98 | 37.66 | 10.0 | 255.0 | 0.9336 | 3.662745 | NaN | 1.572549 |
| 6962 | -118.05 | 33.99 | 38.0 | 357.0 | 3.7328 | 4.535014 | NaN | 2.481793 |
| 14970 | -117.01 | 32.74 | 31.0 | 677.0 | 2.6973 | 5.129985 | NaN | 3.098966 |
| 7763 | -118.10 | 33.91 | 36.0 | 130.0 | 3.6389 | 5.584615 | NaN | 3.769231 |
18576 rows × 8 columns
X_train.shape
X_test.shape
(2064, 8)
imputer = SimpleImputer(strategy="median")
imputer.fit(X_train)
X_train_imp = imputer.transform(X_train)
X_test_imp = imputer.transform(X_test)
Let’s check whether the NaN values have been replaced or not
Note that
imputer.transformreturns annumpyarray and not a dataframe
Scaling#
This problem affects a large number of ML methods.
A number of approaches to this problem. We are going to look into two most popular ones.
Approach |
What it does |
How to update \(X\) (but see below!) |
sklearn implementation |
|---|---|---|---|
standardization |
sets sample mean to \(0\), s.d. to \(1\) |
|
There are all sorts of articles on this; see, e.g. here and here.
# [source](https://amueller.github.io/COMS4995-s19/slides/aml-05-preprocessing/#8)
mglearn.plots.plot_scaling()
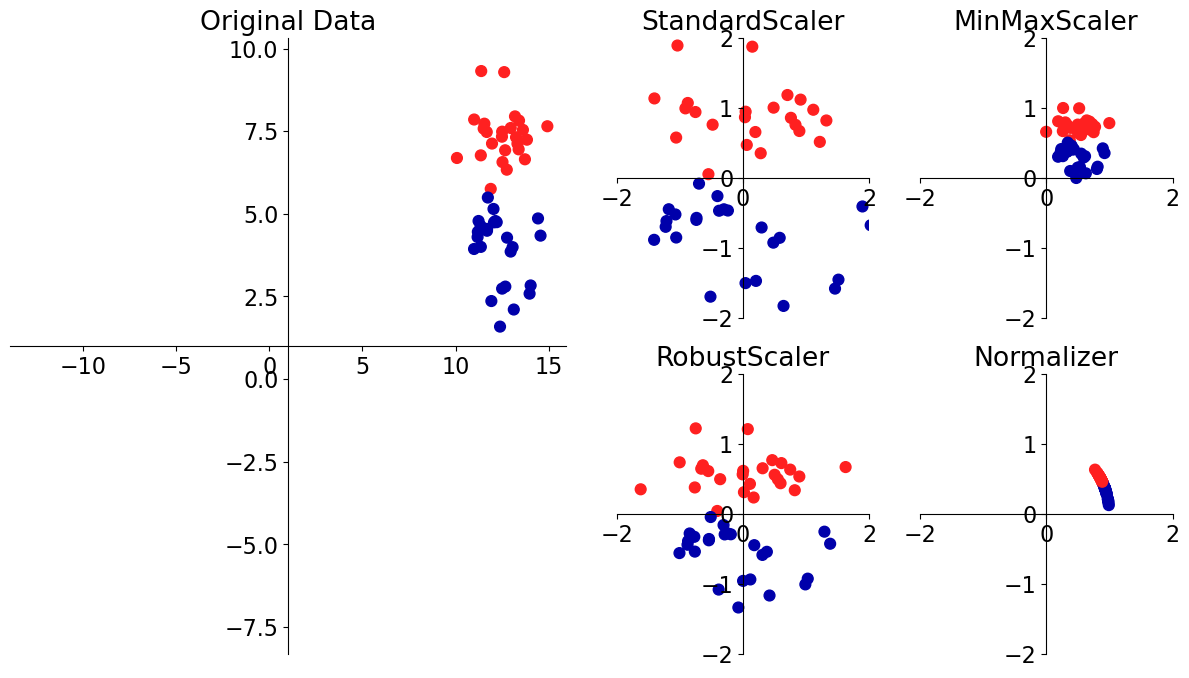
from sklearn.preprocessing import MinMaxScaler, StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_imp)
X_test_scaled = scaler.transform(X_test_imp)
pd.DataFrame(X_train_scaled, columns=X_train.columns)
| longitude | latitude | housing_median_age | households | median_income | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.908140 | -0.743917 | -0.526078 | 0.266135 | -0.389736 | -0.210591 | -0.083813 | 0.126398 |
| 1 | -0.002057 | 1.083123 | -0.923283 | -1.253312 | -0.198924 | 4.726412 | 11.166631 | -0.050132 |
| 2 | 1.218207 | -1.352930 | 1.380504 | 0.542873 | -0.635239 | -0.273606 | -0.025391 | -0.099240 |
| 3 | 1.128188 | -0.753286 | -0.843842 | -0.561467 | 0.714077 | 0.122307 | -0.280310 | 0.010183 |
| 4 | 1.168196 | -1.287344 | -0.843842 | 2.500924 | -1.059242 | -0.640266 | -0.190617 | 0.126808 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 18571 | 0.733102 | -0.804818 | 0.586095 | -0.966131 | -0.118182 | 0.063110 | -0.099558 | 0.071541 |
| 18572 | 1.163195 | -1.057793 | -1.161606 | 0.728235 | 0.357500 | 0.235096 | -0.163397 | 0.007458 |
| 18573 | -1.097293 | 0.797355 | -1.876574 | 0.514155 | 0.934269 | 0.211892 | -0.135305 | 0.044029 |
| 18574 | -1.437367 | 1.008167 | 1.221622 | -0.454427 | 0.006578 | -0.273382 | -0.149822 | -0.132875 |
| 18575 | 0.242996 | 0.272667 | -0.684960 | -0.396991 | -0.711754 | 0.025998 | 0.042957 | 0.051269 |
18576 rows × 8 columns
knn = KNeighborsRegressor()
knn.fit(X_train_scaled, y_train)
knn.score(X_train_scaled, y_train)
0.7978563117812038
Big difference in the KNN training performance after scaling the data.
But we saw last week that training score doesn’t tell us much. We should look at the cross-validation score.
❓❓ Questions for you#
(iClicker) Exercise 5.2#
iClicker cloud join link: https://join.iclicker.com/VYFJ
Select all of the following statements which are TRUE.
StandardScalerensures a fixed range (i.e., minimum and maximum values) for the features.StandardScalercalculates mean and standard deviation for each feature separately.In general, it’s a good idea to apply scaling on numeric features before training \(k\)-NN or SVM RBF models.
The transformed feature values might be hard to interpret for humans.
After applying
SimpleImputerThe transformed data has a different shape than the original data.
Break (5 min)#

Feature transformations and the golden rule#
How to carry out cross-validation?#
Last week we saw that cross validation is a better way to get a realistic assessment of the model.
Let’s try cross-validation with transformed data.
knn = KNeighborsRegressor()
scaler = StandardScaler()
scaler.fit(X_train_imp)
X_train_scaled = scaler.transform(X_train_imp)
X_test_scaled = scaler.transform(X_test_imp)
scores = cross_validate(knn, X_train_scaled, y_train, return_train_score=True)
pd.DataFrame(scores)
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| 0 | 0.003324 | 0.074475 | 0.696373 | 0.794236 |
| 1 | 0.003181 | 0.067119 | 0.684447 | 0.791467 |
| 2 | 0.003166 | 0.073058 | 0.695532 | 0.789436 |
| 3 | 0.003212 | 0.073366 | 0.679478 | 0.793243 |
| 4 | 0.003188 | 0.045415 | 0.680657 | 0.794820 |
Do you see any problem here?
Are we applying
fit_transformon train portion andtransformon validation portion in each fold?Here you might be allowing information from the validation set to leak into the training step.
You need to apply the SAME preprocessing steps to train/validation.
With many different transformations and cross validation the code gets unwieldy very quickly.
Likely to make mistakes and “leak” information.
In these examples our test accuracies look fine, but our methodology is flawed.
Implications can be significant in practice!
Pipelines#
Can we do this in a more elegant and organized way?
YES!! Using
scikit-learn Pipeline.scikit-learn Pipelineallows you to define a “pipeline” of transformers with a final estimator.
Let’s combine the preprocessing and model with pipeline
### Simple example of a pipeline
from sklearn.pipeline import Pipeline
pipe = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="median")),
("scaler", StandardScaler()),
("regressor", KNeighborsRegressor()),
]
)
Syntax: pass in a list of steps.
The last step should be a model/classifier/regressor.
All the earlier steps should be transformers.
Alternative and more compact syntax: make_pipeline#
Shorthand for
PipelineconstructorDoes not permit naming steps
Instead the names of steps are set to lowercase of their types automatically;
StandardScaler()would be named asstandardscaler
from sklearn.pipeline import make_pipeline
pipe = make_pipeline(
SimpleImputer(strategy="median"), StandardScaler(), KNeighborsRegressor()
)
pipe.fit(X_train, y_train)
Pipeline(steps=[('simpleimputer', SimpleImputer(strategy='median')),
('standardscaler', StandardScaler()),
('kneighborsregressor', KNeighborsRegressor())])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Pipeline(steps=[('simpleimputer', SimpleImputer(strategy='median')),
('standardscaler', StandardScaler()),
('kneighborsregressor', KNeighborsRegressor())])SimpleImputer(strategy='median')
StandardScaler()
KNeighborsRegressor()
Note that we are passing
X_trainand not the imputed or scaled data here.
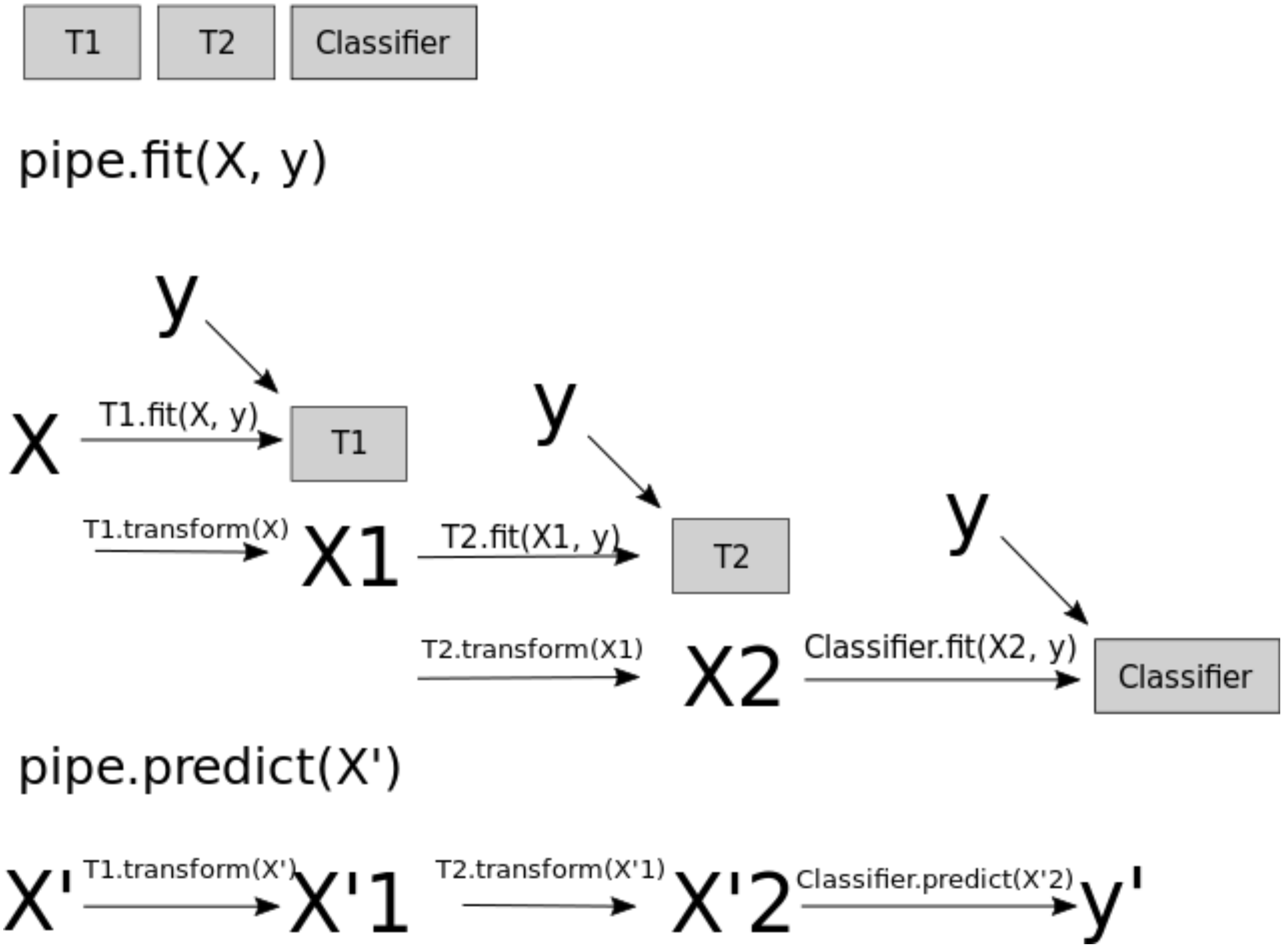
When you call fit on the pipeline, it carries out the following steps:
Fit
SimpleImputeronX_trainTransform
X_trainusing the fitSimpleImputerto createX_train_impFit
StandardScaleronX_train_impTransform
X_train_impusing the fitStandardScalerto createX_train_imp_scaledFit the model (
KNeighborsRegressorin our case) onX_train_imp_scaled
pipe.predict(X_train)
array([126500., 117380., 187700., ..., 259500., 308120., 60860.])
Note that we are passing original data to predict as well. This time the pipeline is carrying out following steps:
Transform
X_trainusing the fitSimpleImputerto createX_train_impTransform
X_train_impusing the fitStandardScalerto createX_train_imp_scaledPredict using the fit model (
KNeighborsRegressorin our case) onX_train_imp_scaled.
Let’s try cross-validation with our pipeline#
results_dict["imp + scaling + knn"] = mean_std_cross_val_scores(
pipe, X_train, y_train, return_train_score=True
)
pd.DataFrame(results_dict).T
/var/folders/b3/g26r0dcx4b35vf3nk31216hc0000gr/T/ipykernel_32469/4158382658.py:26: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
out_col.append((f"%0.3f (+/- %0.3f)" % (mean_scores[i], std_scores[i])))
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| dummy | 0.001 (+/- 0.000) | 0.000 (+/- 0.000) | -0.055 (+/- 0.012) | -0.055 (+/- 0.001) |
| imp + scaling + knn | 0.015 (+/- 0.007) | 0.082 (+/- 0.025) | 0.693 (+/- 0.014) | 0.797 (+/- 0.015) |
Using a Pipeline takes care of applying the fit_transform on the train portion and only transform on the validation portion in each fold.
Categorical features [video]#
Recall that we had dropped the categorical feature
ocean_proximityfeature from the dataframe. But it could potentially be a useful feature in this task.Let’s create our
X_trainand andX_testagain by keeping the feature in the data.
X_train
| longitude | latitude | housing_median_age | households | median_income | rooms_per_household | bedrooms_per_household | population_per_household | |
|---|---|---|---|---|---|---|---|---|
| 6051 | -117.75 | 34.04 | 22.0 | 602.0 | 3.1250 | 4.897010 | 1.056478 | 4.318937 |
| 20113 | -119.57 | 37.94 | 17.0 | 20.0 | 3.4861 | 17.300000 | 6.500000 | 2.550000 |
| 14289 | -117.13 | 32.74 | 46.0 | 708.0 | 2.6604 | 4.738701 | 1.084746 | 2.057910 |
| 13665 | -117.31 | 34.02 | 18.0 | 285.0 | 5.2139 | 5.733333 | 0.961404 | 3.154386 |
| 14471 | -117.23 | 32.88 | 18.0 | 1458.0 | 1.8580 | 3.817558 | 1.004801 | 4.323045 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 7763 | -118.10 | 33.91 | 36.0 | 130.0 | 3.6389 | 5.584615 | NaN | 3.769231 |
| 15377 | -117.24 | 33.37 | 14.0 | 779.0 | 4.5391 | 6.016688 | 1.017972 | 3.127086 |
| 17730 | -121.76 | 37.33 | 5.0 | 697.0 | 5.6306 | 5.958393 | 1.031564 | 3.493544 |
| 15725 | -122.44 | 37.78 | 44.0 | 326.0 | 3.8750 | 4.739264 | 1.024540 | 1.720859 |
| 19966 | -119.08 | 36.21 | 20.0 | 348.0 | 2.5156 | 5.491379 | 1.117816 | 3.566092 |
18576 rows × 8 columns
X_train = train_df.drop(columns=["median_house_value"])
y_train = train_df["median_house_value"]
X_test = test_df.drop(columns=["median_house_value"])
y_test = test_df["median_house_value"]
Let’s try to build a
KNeighborRegressoron this data using our pipeline
# pipe.fit(X_train, X_train)
This failed because we have non-numeric data.
Imagine how \(k\)-NN would calculate distances when you have non-numeric features.
Can we use this feature in the model?#
In
scikit-learn, most algorithms require numeric inputs.Decision trees could theoretically work with categorical features.
However, the sklearn implementation does not support this.
What are the options?#
Drop the column (not recommended)
If you know that the column is not relevant to the target in any way you may drop it.
We can transform categorical features to numeric ones so that we can use them in the model.
Ordinal encoding (occasionally recommended)
One-hot encoding (recommended in most cases) (this lecture)
X_toy = pd.DataFrame(
{
"language": [
"English",
"Vietnamese",
"English",
"Mandarin",
"English",
"English",
"Mandarin",
"English",
"Vietnamese",
"Mandarin",
"French",
"Spanish",
"Mandarin",
"Hindi",
]
}
)
X_toy
| language | |
|---|---|
| 0 | English |
| 1 | Vietnamese |
| 2 | English |
| 3 | Mandarin |
| 4 | English |
| 5 | English |
| 6 | Mandarin |
| 7 | English |
| 8 | Vietnamese |
| 9 | Mandarin |
| 10 | French |
| 11 | Spanish |
| 12 | Mandarin |
| 13 | Hindi |
Ordinal encoding (occasionally recommended)#
Here we simply assign an integer to each of our unique categorical labels.
We can use sklearn’s
OrdinalEncoder.
from sklearn.preprocessing import OrdinalEncoder
enc = OrdinalEncoder()
enc.fit(X_toy)
X_toy_ord = enc.transform(X_toy)
df = pd.DataFrame(
data=X_toy_ord,
columns=["language_enc"],
index=X_toy.index,
)
pd.concat([X_toy, df], axis=1)
| language | language_enc | |
|---|---|---|
| 0 | English | 0.0 |
| 1 | Vietnamese | 5.0 |
| 2 | English | 0.0 |
| 3 | Mandarin | 3.0 |
| 4 | English | 0.0 |
| 5 | English | 0.0 |
| 6 | Mandarin | 3.0 |
| 7 | English | 0.0 |
| 8 | Vietnamese | 5.0 |
| 9 | Mandarin | 3.0 |
| 10 | French | 1.0 |
| 11 | Spanish | 4.0 |
| 12 | Mandarin | 3.0 |
| 13 | Hindi | 2.0 |
What’s the problem with this approach?
We have imposed ordinality on the categorical data.
For example, imagine when you are calculating distances. Is it fair to say that French and Hindi are closer than French and Spanish?
In general, label encoding is useful if there is ordinality in your data and capturing it is important for your problem, e.g.,
[cold, warm, hot].
One-hot encoding (OHE)#
Create new binary columns to represent our categories.
If we have \(c\) categories in our column.
We create \(c\) new binary columns to represent those categories.
Example: Imagine a language column which has the information on whether you
We can use sklearn’s
OneHotEncoderto do so.
Note
One-hot encoding is called one-hot because only one of the newly created features is 1 for each data point.
from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
enc.fit(X_toy)
X_toy_ohe = enc.transform(X_toy)
pd.DataFrame(
data=X_toy_ohe,
columns=enc.get_feature_names_out(["language"]),
index=X_toy.index,
)
| language_English | language_French | language_Hindi | language_Mandarin | language_Spanish | language_Vietnamese | |
|---|---|---|---|---|---|---|
| 0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 2 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 3 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 4 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 5 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 6 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 7 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 9 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 10 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 11 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 12 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 13 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
Let’s do it on our housing data#
ohe = OneHotEncoder(sparse_output=False, dtype="int")
ohe.fit(X_train[["ocean_proximity"]])
X_imp_ohe_train = ohe.transform(X_train[["ocean_proximity"]])
We can look at the new features created using
categories_attribute
ohe.categories_
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]
transformed_ohe = pd.DataFrame(
data=X_imp_ohe_train,
columns=ohe.get_feature_names_out(["ocean_proximity"]),
index=X_train.index,
)
transformed_ohe
| ocean_proximity_<1H OCEAN | ocean_proximity_INLAND | ocean_proximity_ISLAND | ocean_proximity_NEAR BAY | ocean_proximity_NEAR OCEAN | |
|---|---|---|---|---|---|
| 6051 | 0 | 1 | 0 | 0 | 0 |
| 20113 | 0 | 1 | 0 | 0 | 0 |
| 14289 | 0 | 0 | 0 | 0 | 1 |
| 13665 | 0 | 1 | 0 | 0 | 0 |
| 14471 | 0 | 0 | 0 | 0 | 1 |
| ... | ... | ... | ... | ... | ... |
| 7763 | 1 | 0 | 0 | 0 | 0 |
| 15377 | 1 | 0 | 0 | 0 | 0 |
| 17730 | 1 | 0 | 0 | 0 | 0 |
| 15725 | 0 | 0 | 0 | 1 | 0 |
| 19966 | 0 | 1 | 0 | 0 | 0 |
18576 rows × 5 columns
See also
One-hot encoded variables are also referred to as dummy variables.
You will often see people using get_dummies method of pandas to convert categorical variables into dummy variables. That said, using sklearn’s OneHotEncoder has the advantage of making it easy to treat training and test set in a consistent way.
❓❓ Questions for you#
(iClicker) Exercise 5.3#
iClicker cloud join link: https://join.iclicker.com/VYFJ
Select all of the following statements which are TRUE.
You can have scaling of numeric features, one-hot encoding of categorical features, and
scikit-learnestimator within a single pipeline.Once you have a
scikit-learnpipeline object with an estimator as the last step, you can callfit,predict, andscoreon it.You can carry out data splitting within
scikit-learnpipeline.We have to be careful of the order we put each transformation and model in a pipeline.
If you call
cross_validatewith a pipeline object, it will callfitandtransformon the training fold and onlytransformon the validation fold.
What did we learn today?#
Motivation for preprocessing
Common preprocessing steps
Imputation
Scaling
One-hot encoding
Golden rule in the context of preprocessing
Building simple supervised machine learning pipelines using
sklearn.pipeline.make_pipeline.
Problem: Different transformations on different columns#
How do we put this together with other columns in the data before fitting the regressor?
Before we fit our regressor, we want to apply different transformations on different columns
Numeric columns
imputation
scaling
Categorical columns
imputation
one-hot encoding
Coming up: sklearn’s ColumnTransformer!!
