
Lecture 12: Ensembles#
UBC 2024-25
The interests of truth require a diversity of opinions.by John Stuart Mill
Imports, announcements, LOs#
Imports#
import os
%matplotlib inline
import string
import sys
from collections import deque
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
sys.path.append(os.path.join(os.path.abspath(".."), "code"))
from plotting_functions import *
from sklearn import datasets
from sklearn.compose import ColumnTransformer, make_column_transformer
from sklearn.dummy import DummyClassifier, DummyRegressor
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import (
GridSearchCV,
RandomizedSearchCV,
cross_val_score,
cross_validate,
train_test_split,
)
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.preprocessing import OneHotEncoder, OrdinalEncoder, StandardScaler
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from utils import *
DATA_DIR = os.path.join(os.path.abspath(".."), "data/")
Lecture learning objectives#
From this lecture, you will be able to
Broadly explain the idea of ensembles
Explain how does predict work in the context of random forest models
Explain the sources of randomness in random forest algorithm
Explain the relation between number of estimators and the fundamental tradeoff in the context of random forests
Use
scikit-learn’s random forest classification and regression models and explain their main hyperparametersUse other tree-based models such as as
XGBoost,LGBMandCatBoostBroadly explain ensemble approaches, in particular model averaging and stacking.
Use
scikit-learnimplementations of these ensemble methods.
Motivation [video]#
❓❓ Questions for you#
iClicker Exercise 12.0#
iClicker cloud join link: https://join.iclicker.com/VYFJ
Which of the following scenarios has worked effectively for you in the past?
(A) Working independently on a project/assignment.
(B) Working with like-minded people.
(C) Teaming up with a diverse group offering varied perspectives and skills.
Ensembles are models that combine multiple machine learning models to create more powerful models.
The Netflix prize#
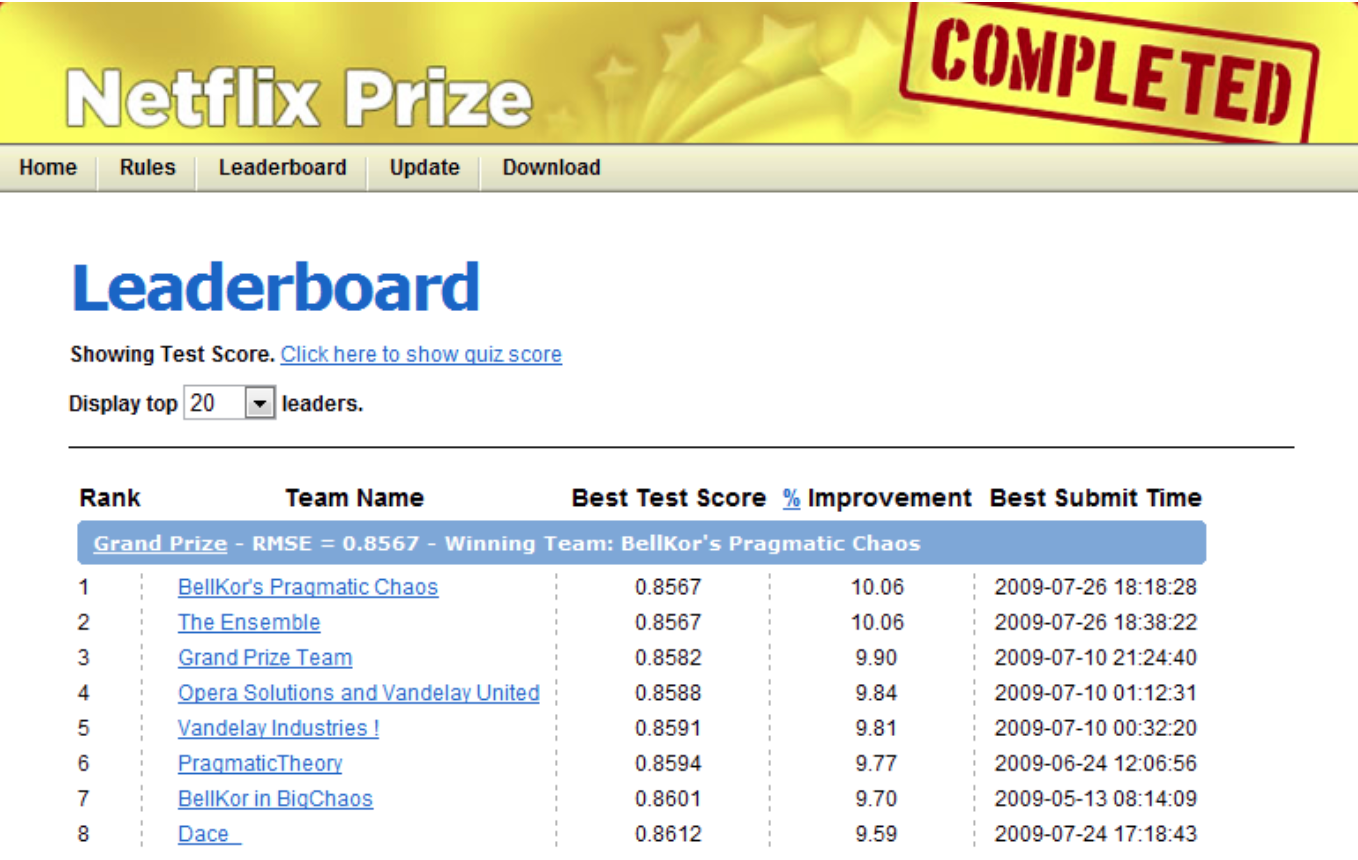
Read the story here.
Most of the winning solutions for Kaggle competitions involve some kind of ensembling. For example:
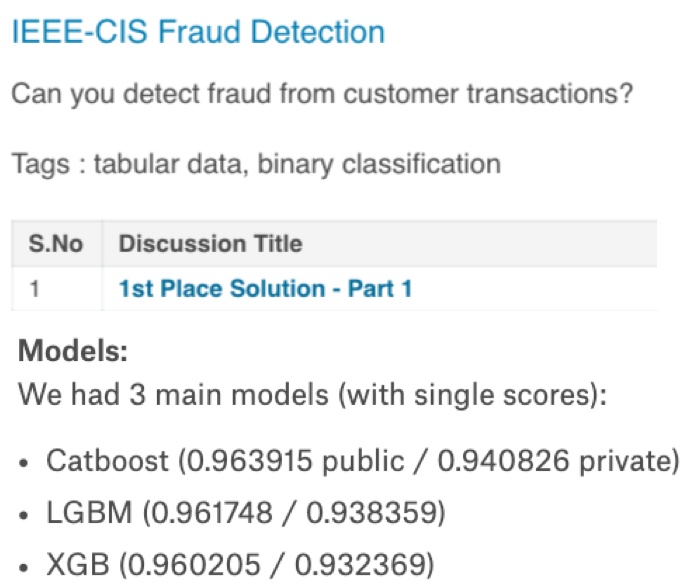
Key idea: Groups can often make better decisions than individuals, especially when group members are diverse enough.

Tree-based ensemble models#
A number of ensemble models in ML literature.
Most successful ones on a variety of datasets are tree-based models.
We’ll briefly talk about two such models:
Random forests
Gradient boosted trees
We’ll also talk about averaging and stacking.
Tree-based models#
Decision trees models are
Interpretable
They can capture non-linear relationships
They don’t require scaling of the data and theoretically can work with categorical features and missing values.
But single decision trees are likely to overfit.
Key idea: Combine multiple trees to build stronger models.
These kinds of models are extremely popular in industry and machine learning competitions.
We are going to cover how to use a few popular tree-based models:
Random forests
Gradient boosted trees (very high level)
We will also talk about two common ways to combine different models:
Averaging
Stacking
Data#
Let’s work with the adult census data set.
adult_df_large = pd.read_csv(DATA_DIR + "adult.csv")
train_df, test_df = train_test_split(adult_df_large, test_size=0.2, random_state=42)
train_df_nan = train_df.replace("?", np.NaN)
test_df_nan = test_df.replace("?", np.NaN)
train_df_nan.head()
| age | workclass | fnlwgt | education | education.num | marital.status | occupation | relationship | race | sex | capital.gain | capital.loss | hours.per.week | native.country | income | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5514 | 26 | Private | 256263 | HS-grad | 9 | Never-married | Craft-repair | Not-in-family | White | Male | 0 | 0 | 25 | United-States | <=50K |
| 19777 | 24 | Private | 170277 | HS-grad | 9 | Never-married | Other-service | Not-in-family | White | Female | 0 | 0 | 35 | United-States | <=50K |
| 10781 | 36 | Private | 75826 | Bachelors | 13 | Divorced | Adm-clerical | Unmarried | White | Female | 0 | 0 | 40 | United-States | <=50K |
| 32240 | 22 | State-gov | 24395 | Some-college | 10 | Married-civ-spouse | Adm-clerical | Wife | White | Female | 0 | 0 | 20 | United-States | <=50K |
| 9876 | 31 | Local-gov | 356689 | Bachelors | 13 | Married-civ-spouse | Prof-specialty | Husband | White | Male | 0 | 0 | 40 | United-States | <=50K |
numeric_features = ["age", "capital.gain", "capital.loss", "hours.per.week"]
categorical_features = [
"workclass",
"marital.status",
"occupation",
"relationship",
"native.country",
]
ordinal_features = ["education"]
binary_features = ["sex"]
drop_features = ["fnlwgt", "race", "education.num"]
target_column = "income"
education_levels = [
"Preschool",
"1st-4th",
"5th-6th",
"7th-8th",
"9th",
"10th",
"11th",
"12th",
"HS-grad",
"Prof-school",
"Assoc-voc",
"Assoc-acdm",
"Some-college",
"Bachelors",
"Masters",
"Doctorate",
]
assert set(education_levels) == set(train_df["education"].unique())
numeric_transformer = StandardScaler()
ordinal_transformer = OrdinalEncoder(categories=[education_levels], dtype=int)
binary_transformer = make_pipeline(
SimpleImputer(strategy="constant", fill_value="missing"),
OneHotEncoder(drop="if_binary", dtype=int),
)
categorical_transformer = make_pipeline(
SimpleImputer(strategy="constant", fill_value="missing"),
OneHotEncoder(handle_unknown="ignore", sparse_output=False),
)
preprocessor = make_column_transformer(
(numeric_transformer, numeric_features),
(ordinal_transformer, ordinal_features),
(binary_transformer, binary_features),
(categorical_transformer, categorical_features),
("drop", drop_features),
)
preprocessor
ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])['age', 'capital.gain', 'capital.loss', 'hours.per.week']
StandardScaler()
['education']
OrdinalEncoder(categories=[['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th',
'10th', '11th', '12th', 'HS-grad', 'Prof-school',
'Assoc-voc', 'Assoc-acdm', 'Some-college',
'Bachelors', 'Masters', 'Doctorate']],
dtype=<class 'int'>)['sex']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(drop='if_binary', dtype=<class 'int'>)
['workclass', 'marital.status', 'occupation', 'relationship', 'native.country']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
['fnlwgt', 'race', 'education.num']
drop
X_train = train_df_nan.drop(columns=[target_column])
y_train = train_df_nan[target_column]
X_test = test_df_nan.drop(columns=[target_column])
y_test = test_df_nan[target_column]
Do we have class imbalance?#
There is class imbalance. But without any context, both classes seem equally important.
Let’s use accuracy as our metric.
train_df["income"].value_counts(normalize=True)
income
<=50K 0.757985
>50K 0.242015
Name: proportion, dtype: float64
scoring_metric = "accuracy"
We are going to use models outside sklearn. Some of them cannot handle categorical target values. So we’ll convert them to integers using LabelEncoder.
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
y_train_num = label_encoder.fit_transform(y_train)
y_test_num = label_encoder.transform(y_test)
y_train_num
array([0, 0, 0, ..., 1, 1, 0])
Let’s store all the results in a dictionary called results.
results = {}
Baselines#
DummyClassifier baseline#
dummy = DummyClassifier()
results["Dummy"] = mean_std_cross_val_scores(
dummy, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
)
DecisionTreeClassifier baseline#
Let’s try decision tree classifier on our data.
pipe_dt = make_pipeline(preprocessor, DecisionTreeClassifier(random_state=123))
results["Decision tree"] = mean_std_cross_val_scores(
pipe_dt, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
)
pd.DataFrame(results).T
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| Dummy | 0.006 (+/- 0.003) | 0.001 (+/- 0.001) | 0.758 (+/- 0.000) | 0.758 (+/- 0.000) |
| Decision tree | 0.141 (+/- 0.027) | 0.012 (+/- 0.001) | 0.817 (+/- 0.006) | 0.979 (+/- 0.000) |
Decision tree is clearly overfitting.
Random forests#

General idea#
A single decision tree is likely to overfit
Use a collection of diverse decision trees
Each tree overfits on some part of the data but we can reduce overfitting by averaging the results
can be shown mathematically
RandomForestClassifier#
Before understanding the details let’s first try it out.
from sklearn.ensemble import RandomForestClassifier
pipe_rf = make_pipeline(
preprocessor,
RandomForestClassifier(
n_jobs=-1,
random_state=123,
),
)
results["Random forests"] = mean_std_cross_val_scores(
pipe_rf, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
)
pd.DataFrame(results).T
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| Dummy | 0.006 (+/- 0.003) | 0.001 (+/- 0.001) | 0.758 (+/- 0.000) | 0.758 (+/- 0.000) |
| Decision tree | 0.141 (+/- 0.027) | 0.012 (+/- 0.001) | 0.817 (+/- 0.006) | 0.979 (+/- 0.000) |
| Random forests | 0.442 (+/- 0.119) | 0.039 (+/- 0.002) | 0.847 (+/- 0.006) | 0.979 (+/- 0.000) |
The validation scores are better although it seems likes we are still overfitting.
How do they work?#
Decide how many decision trees we want to build
can control with
n_estimatorshyperparameter
fita diverse set of that many decision trees by injecting randomness in the model constructionpredictby voting (classification) or averaging (regression) of predictions given by individual models
Inject randomness in the classifier construction#
To ensure that the trees in the random forest are different we inject randomness in two ways:
Data: Build each tree on a bootstrap sample (i.e., a sample drawn with replacement from the training set)
Features: At each node, select a random subset of features (controlled by
max_featuresinscikit-learn) and look for the best possible test involving one of these features
An example of a bootstrap samples#
Suppose you are training a random forest model with
n_estimators=3.Suppose this is your original dataset with six examples: [0,1,2,3,4,5]
a sample drawn with replacement for tree 1: [1,1,3,3,3,4]
a sample drawn with replacement for tree 2: [3,2,2,2,1,1]
a sample drawn with replacement for tree 3: [0,0,0,4,4,5]
Each decision tree trains on a total of six examples.
Each tree trains on a different set of examples.
random_forest_data = {'original':[1, 1, 1, 1, 1, 1], 'tree1':[0, 2, 0, 3, 1, 0], 'tree2':[0, 2, 3, 1, 0, 0], 'tree3':[3, 0, 0, 0, 2, 1]}
pd.DataFrame(random_forest_data)
| original | tree1 | tree2 | tree3 | |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 3 |
| 1 | 1 | 2 | 2 | 0 |
| 2 | 1 | 0 | 3 | 0 |
| 3 | 1 | 3 | 1 | 0 |
| 4 | 1 | 1 | 0 | 2 |
| 5 | 1 | 0 | 0 | 1 |
The random forests classifier#
Create a collection (ensemble) of trees. Grow each tree on an independent bootstrap sample from the data.
At each node:
Randomly select a subset of features out of all features (independently for each node).
Find the best split on the selected features.
Grow the trees to maximum depth.
Prediction time
Vote the trees to get predictions for new example.
Example#
Let’s create a random forest with 3 estimators.
I’m using
max_depth=2for easy visualization.
pipe_rf_demo = make_pipeline(
preprocessor, RandomForestClassifier(max_depth=2, n_estimators=3, random_state=123)
)
pipe_rf_demo.fit(X_train, y_train_num);
Let’s get the feature names of transformed features.
feature_names = (
numeric_features
+ ordinal_features
+ binary_features
+ pipe_rf_demo.named_steps["columntransformer"]
.named_transformers_["pipeline-2"]
.named_steps["onehotencoder"]
.get_feature_names_out(categorical_features)
.tolist()
)
feature_names[:10]
['age',
'capital.gain',
'capital.loss',
'hours.per.week',
'education',
'sex',
'workclass_Federal-gov',
'workclass_Local-gov',
'workclass_Never-worked',
'workclass_Private']
Let’s sample a test example where income > 50k.
probs = pipe_rf_demo.predict_proba(X_test)
np.where(probs[:, 1] > 0.55)
(array([ 582, 1271, 1991, 2268, 2447, 2516, 2556, 4151, 4165, 5294, 5798,
5970, 6480]),)
test_example = X_test.iloc[[582]]
pipe_rf_demo.predict_proba(test_example)
print("Classes: ", pipe_rf_demo.classes_)
print("Prediction by random forest: ", pipe_rf_demo.predict(test_example))
transformed_example = preprocessor.transform(test_example)
pd.DataFrame(data=transformed_example.flatten(), index=feature_names)
Classes: [0 1]
Prediction by random forest: [1]
| 0 | |
|---|---|
| age | 0.550004 |
| capital.gain | -0.147166 |
| capital.loss | -0.217680 |
| hours.per.week | 1.579660 |
| education | 15.000000 |
| ... | ... |
| native.country_Trinadad&Tobago | 0.000000 |
| native.country_United-States | 1.000000 |
| native.country_Vietnam | 0.000000 |
| native.country_Yugoslavia | 0.000000 |
| native.country_missing | 0.000000 |
85 rows × 1 columns
We can look at different trees created by random forest.
Note that each tree looks at different set of features and slightly different data.
for i, tree in enumerate(
pipe_rf_demo.named_steps["randomforestclassifier"].estimators_
):
print("\n\nTree", i + 1)
display(custom_plot_tree(tree, feature_names, fontsize=12))
print("prediction", tree.predict(preprocessor.transform(test_example)))
Tree 1
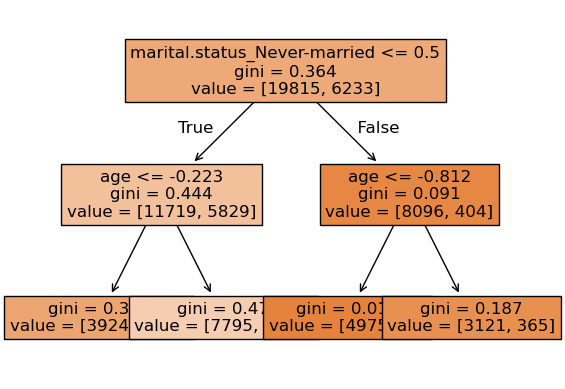
None
prediction [0.]
Tree 2
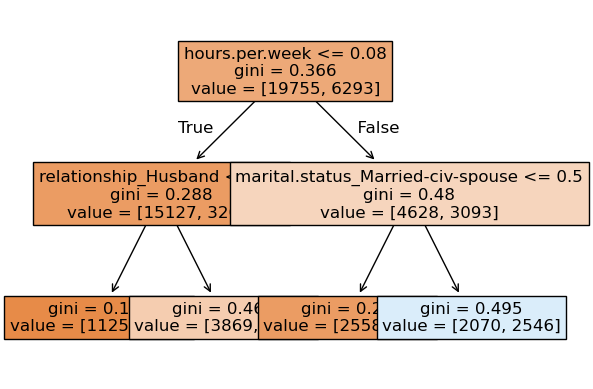
None
prediction [1.]
Tree 3
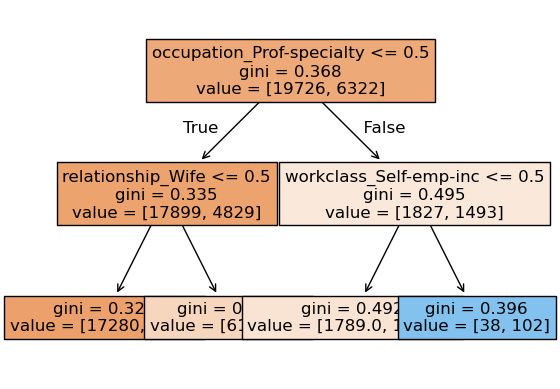
None
prediction [1.]
Some important hyperparameters:#
n_estimators: number of decision trees (higher = more complexity)max_depth: max depth of each decision tree (higher = more complexity)max_features: the number of features you get to look at each split (higher = more complexity)
Random forests: number of trees (n_estimators) and the fundamental tradeoff#
make_num_tree_plot(
preprocessor, X_train, y_train, X_test, y_test, [1, 5, 10, 25, 50, 100, 200, 500]
) # User-defined function defined in code/plotting_functions.py
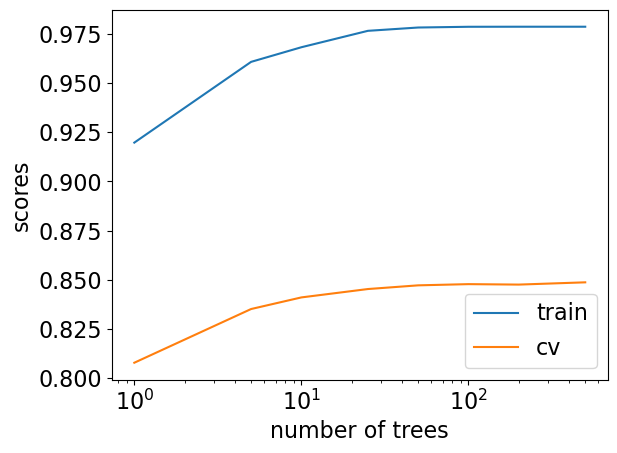
Number of trees and fundamental trade-off#
Above: seems like we’re beating the fundamental “tradeoff” by increasing training score and not decreasing validation score much.
You’ll often see a high training scores for in the context of random forests. That’s normal. It doesn’t mean that the model is overfitting.
While ensembles often offer improved performance, this benefit isn’t always guaranteed.
Always opting for more trees in a random forest is preferable, but we sometimes choose fewer trees for faster performance.
Strengths and weaknesses#
Usually one of the best performing off-the-shelf classifiers without heavy tuning of hyperparameters
Don’t require scaling of data
Less likely to overfit
Slower than decision trees because we are fitting multiple trees but can easily parallelize training because all trees are independent of each other
In general, able to capture a much broader picture of the data compared to a single decision tree.
Weaknesses#
Require more memory
Hard to interpret
Tend not to perform well on high dimensional sparse data such as text data
See also
There is also something called ExtraTreesClassifier where randomness goes one step further in the way splits are computed. As in random forests, a random subset of candidate features is used, but instead of looking for the most discriminative thresholds, thresholds are drawn at random for each candidate feature and the best of these randomly-generated thresholds is picked as the splitting rule.
Source
Important
Make sure to set the random_state for reproducibility. Changing the random_state can have a big impact on the model and the results due to the random nature of these models. Having more trees can get you a more robust estimate.
See also
The original random forests paper by Leo Breiman.
❓❓ Questions for you#
iClicker Exercise 12.1#
iClicker cloud join link: https://join.iclicker.com/VYFJ
Select the true statements from the list below.
(A) Every tree in a random forest uses a different bootstrap sample of the training set.
(B) To train a tree in a random forest, we first randomly select a subset of features. The tree is then restricted to only using those features.
(C) The
n_estimatorshyperparameter of random forests should be tuned to get a better performance on the validation or test data.(D) In random forests we build trees in a sequential fashion, where the current tree is dependent upon the previous tree.
(E) Random forest decisions are interpretable (i.e. it is possible to say how a feature value impacted the classification of a sample).
Why do we create random forests out of random trees (trees where each stump only looks at a subset of the features, and the dataset is a bootstrap sample) rather than creating them out of regular decision trees?
Gradient boosted trees [video]#
Another popular and effective class of tree-based models is gradient boosted trees.
No randomization.
The key idea is combining many simple models called weak learners to create a strong learner.
They combine multiple shallow (depth 1 to 5) decision trees.
They build trees in a serial manner, where each tree tries to correct the mistakes of the previous one.
(Optional) Prediction in boosted regression trees#
Credit: Adapted from CPSC 340 notes
Gradient boosting starts with an ensemble of \(k\) shallow decision trees.
For each example \(i\), each shallow tree makes a continuous prediction: \(\hat{y}_{i1}, \hat{y}_{i2}, \dots, \hat{y}_{ik}\)
The final prediction is sum of individual predictions: \(\hat{y}_{i1} + \hat{y}_{i2} + \dots + \hat{y}_{ik}\)
Note that we do not use the average as we would with random forests because
In boosting, each tree is not individually trying to predict the true \(y_i\) value
Instead, each new tree tries to “fix” the prediction made by the old trees, so that sum is \(y_i\)
(Optional) Fitting in boosted regression trees.#
Consider the following “gradient tree boosting” procedure:
Tree[1].fit(X,y)
y_hat = Tree[1].predict(X)
Tree[2].fit(X,y - y_hat)
y_hat = y_hat + Tree[2].predict(X)
Tree[3].fit(X,y - y_hat)
y_hat = y_hat + Tree[3].predict(X)
Tree[4].fit(X,y - y_hat)
y_hat = y_hat + Tree[4].predict(X)
Each tree is trying to predict residuals (
y - y_hat) of current prediction.True label is 0.9, old prediction is 0.8, so I can improve
y_hatby predicting 0.1.
We’ll not go into the details. If you want to know more, here are some resources:
We’ll look at brief examples of using the following three gradient boosted tree models.
XGBoost#
Not part of
sklearnbut has similar interface.Install it in your conda environment:
conda install -c conda-forge xgboostSupports missing values
GPU training, networked parallel training
Supports sparse data
Typically better scores than random forests
LightGBM#
Not part of
sklearnbut has similar interface.Install it in your conda environment:
conda install -c conda-forge lightgbmSmall model size
Faster
Typically better scores than random forests
CatBoost#
Not part of
sklearnbut has similar interface.Install it in your course conda environment:
conda install -c conda-forge catboostUsually better scores but slower compared to
XGBoostandLightGBM
Important hyperparameters#
n_estimators\(\rightarrow\) Number of boosting roundslearning_rate\(\rightarrow\) The learning rate of trainingcontrols how strongly each tree tries to correct the mistakes of the previous trees
higher learning rate means each tree can make stronger corrections, which means more complex model
max_depth\(\rightarrow\)max_depthof trees (similar to decision trees)scale_pos_weight\(\rightarrow\) Balancing of positive and negative weights
In our demo below, we’ll just give equal weight to both classes because we are trying to optimize accuracy. But if you want to give more weight to class 1, for example, you can calculate the data imbalance ratio and set scale_pos_weight hyperparameter with that weight.
ratio = np.bincount(y_train_num)[0] / np.bincount(y_train_num)[1]
ratio
3.1319796954314723
Gradient boosting in sklearn#
sklearn also has gradient boosting models.
HistGradientBoostingClassifier and HistGradientBoostingRegressor (Inspired by LGBM, supports missing values)
Let’s try out all these models.
conda install -c conda-forge lightgbm
Collecting package metadata (current_repodata.json): | WARNING conda.models.version:get_matcher(556): Using .* with relational operator is superfluous and deprecated and will be removed in a future version of conda. Your spec was 1.7.1.*, but conda is ignoring the .* and treating it as 1.7.1
done
Solving environment: done
==> WARNING: A newer version of conda exists. <==
current version: 23.9.0
latest version: 24.9.2
Please update conda by running
$ conda update -n base -c conda-forge conda
Or to minimize the number of packages updated during conda update use
conda install conda=24.9.2
## Package Plan ##
environment location: /Users/gtoti/opt/anaconda3/envs/cpsc330-24
added / updated specs:
- lightgbm
The following packages will be downloaded:
package | build
---------------------------|-----------------
lightgbm-4.5.0 |cpu_py3.12h3b4354a_2 1.6 MB conda-forge
------------------------------------------------------------
Total: 1.6 MB
The following packages will be UPDATED:
lightgbm 4.5.0-cpu_py3.12h1b86e91_1 --> 4.5.0-cpu_py3.12h3b4354a_2
Downloading and Extracting Packages:
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
Note: you may need to restart the kernel to use updated packages.
from catboost import CatBoostClassifier
from lightgbm.sklearn import LGBMClassifier
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
from sklearn.ensemble import GradientBoostingClassifier, HistGradientBoostingClassifier
pipe_lr = make_pipeline(
preprocessor, LogisticRegression(max_iter=2000, random_state=123)
)
pipe_dt = make_pipeline(preprocessor, DecisionTreeClassifier(random_state=123))
pipe_rf = make_pipeline(
preprocessor, RandomForestClassifier(class_weight="balanced", random_state=123)
)
pipe_xgb = make_pipeline(
preprocessor,
XGBClassifier(
random_state=123, verbosity=0
),
)
pipe_lgbm = make_pipeline(
preprocessor, LGBMClassifier(random_state=123, verbose=-1)
)
pipe_catboost = make_pipeline(
preprocessor,
CatBoostClassifier(verbose=0, random_state=123),
)
pipe_sklearn_histGB = make_pipeline(
preprocessor,
HistGradientBoostingClassifier(random_state=123),
)
pipe_sklearn_GB = make_pipeline(
preprocessor,
GradientBoostingClassifier(random_state=123),
)
classifiers = {
"logistic regression": pipe_lr,
"decision tree": pipe_dt,
"random forest": pipe_rf,
"XGBoost": pipe_xgb,
"LightGBM": pipe_lgbm,
"CatBoost": pipe_catboost,
"sklearn_histGB": pipe_sklearn_histGB,
"sklearn_GB": pipe_sklearn_GB,
}
import warnings
warnings.simplefilter(action="ignore", category=DeprecationWarning)
warnings.simplefilter(action="ignore", category=UserWarning)
results = {}
dummy = DummyClassifier()
results["Dummy"] = mean_std_cross_val_scores(
dummy, X_train, y_train, return_train_score=True, scoring=scoring_metric
)
for (name, model) in classifiers.items():
results[name] = mean_std_cross_val_scores(
model, X_train, y_train_num, return_train_score=True, scoring=scoring_metric
)
pd.DataFrame(results).T
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| Dummy | 0.014 (+/- 0.004) | 0.010 (+/- 0.001) | 0.758 (+/- 0.000) | 0.758 (+/- 0.000) |
| logistic regression | 0.470 (+/- 0.088) | 0.013 (+/- 0.001) | 0.849 (+/- 0.005) | 0.850 (+/- 0.001) |
| decision tree | 0.131 (+/- 0.007) | 0.012 (+/- 0.001) | 0.817 (+/- 0.006) | 0.979 (+/- 0.000) |
| random forest | 1.445 (+/- 0.025) | 0.077 (+/- 0.001) | 0.844 (+/- 0.007) | 0.976 (+/- 0.001) |
| XGBoost | 0.224 (+/- 0.021) | 0.016 (+/- 0.001) | 0.871 (+/- 0.005) | 0.899 (+/- 0.002) |
| LightGBM | 0.228 (+/- 0.064) | 0.026 (+/- 0.003) | 0.872 (+/- 0.004) | 0.888 (+/- 0.000) |
| CatBoost | 5.158 (+/- 0.037) | 0.211 (+/- 0.002) | 0.872 (+/- 0.003) | 0.895 (+/- 0.001) |
| sklearn_histGB | 0.904 (+/- 0.125) | 0.027 (+/- 0.002) | 0.871 (+/- 0.005) | 0.887 (+/- 0.002) |
| sklearn_GB | 2.084 (+/- 0.035) | 0.016 (+/- 0.001) | 0.864 (+/- 0.004) | 0.870 (+/- 0.001) |
Some observations
Keep in mind all these results are with default hyperparameters
Ideally we would carry out hyperparameter optimization for all of them and then compare the results.
We are using a particular scoring metric (accuracy in this case)
We are scaling numeric features but it shouldn’t matter for tree-based models
Look at the standard deviation. Doesn’t look very high.
The scores look more or less stable.
Decision trees and random forests overfit
Other models do not seem to overfit much.
Fit times
Decision trees are fast but not very accurate
LightGBM is faster than decision trees and more accurate!
CatBoost fit time is highest.
There is not much difference between the validation scores of XGBoost, LightGBM, and CatBoost.
Among the best performing models, LightGBM is the fastest one!
Scores times
Prediction times are much smaller in all cases.
Which model should I use?#
Simple answer
Whichever gets the highest CV score making sure that you’re not overusing the validation set.
Interpretability
This is an area of growing interest and concern in ML.
How important is interpretability for you?
In the next class we’ll talk about interpretability of non-linear models.
Speed/code maintenance
Other considerations could be speed (fit and/or predict), maintainability of the code.
Finally, you could use all of them!
Averaging#
Earlier we looked at a bunch of classifiers:
classifiers.keys()
dict_keys(['logistic regression', 'decision tree', 'random forest', 'XGBoost', 'LightGBM', 'CatBoost', 'sklearn_histGB', 'sklearn_GB'])
For this demonstration, let’s get rid of sklearn’s gradient boosting models and CatBoost because it’s too slow.
del classifiers["sklearn_histGB"]
del classifiers["sklearn_GB"]
del classifiers["CatBoost"]
classifiers.keys()
dict_keys(['logistic regression', 'decision tree', 'random forest', 'XGBoost', 'LightGBM'])
What if we use all the models in classifiers and let them vote during prediction time?
from sklearn.ensemble import VotingClassifier
averaging_model = VotingClassifier(
list(classifiers.items()), voting="soft"
) # need the list() here for cross-validation to work!
from sklearn import set_config
set_config(display="diagram") # global setting
averaging_model
VotingClassifier(estimators=[('logistic regression',
Pipeline(steps=[('columntransformer',
ColumnTransformer(transformers=[('standardscaler',
StandardScaler(),
['age',
'capital.gain',
'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th',
'9th',
'10th',
'11th',
'12th',
'HS-grad',
'Prof-school',...
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass',
'marital.status',
'occupation',
'relationship',
'native.country']),
('drop',
'drop',
['fnlwgt',
'race',
'education.num'])])),
('lgbmclassifier',
LGBMClassifier(random_state=123,
verbose=-1))]))],
voting='soft')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
VotingClassifier(estimators=[('logistic regression',
Pipeline(steps=[('columntransformer',
ColumnTransformer(transformers=[('standardscaler',
StandardScaler(),
['age',
'capital.gain',
'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th',
'9th',
'10th',
'11th',
'12th',
'HS-grad',
'Prof-school',...
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass',
'marital.status',
'occupation',
'relationship',
'native.country']),
('drop',
'drop',
['fnlwgt',
'race',
'education.num'])])),
('lgbmclassifier',
LGBMClassifier(random_state=123,
verbose=-1))]))],
voting='soft')ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])['age', 'capital.gain', 'capital.loss', 'hours.per.week']
StandardScaler()
['education']
OrdinalEncoder(categories=[['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th',
'10th', '11th', '12th', 'HS-grad', 'Prof-school',
'Assoc-voc', 'Assoc-acdm', 'Some-college',
'Bachelors', 'Masters', 'Doctorate']],
dtype=<class 'int'>)['sex']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(drop='if_binary', dtype=<class 'int'>)
['workclass', 'marital.status', 'occupation', 'relationship', 'native.country']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
['fnlwgt', 'race', 'education.num']
drop
LogisticRegression(max_iter=2000, random_state=123)
ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])['age', 'capital.gain', 'capital.loss', 'hours.per.week']
StandardScaler()
['education']
OrdinalEncoder(categories=[['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th',
'10th', '11th', '12th', 'HS-grad', 'Prof-school',
'Assoc-voc', 'Assoc-acdm', 'Some-college',
'Bachelors', 'Masters', 'Doctorate']],
dtype=<class 'int'>)['sex']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(drop='if_binary', dtype=<class 'int'>)
['workclass', 'marital.status', 'occupation', 'relationship', 'native.country']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
['fnlwgt', 'race', 'education.num']
drop
DecisionTreeClassifier(random_state=123)
ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])['age', 'capital.gain', 'capital.loss', 'hours.per.week']
StandardScaler()
['education']
OrdinalEncoder(categories=[['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th',
'10th', '11th', '12th', 'HS-grad', 'Prof-school',
'Assoc-voc', 'Assoc-acdm', 'Some-college',
'Bachelors', 'Masters', 'Doctorate']],
dtype=<class 'int'>)['sex']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(drop='if_binary', dtype=<class 'int'>)
['workclass', 'marital.status', 'occupation', 'relationship', 'native.country']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
['fnlwgt', 'race', 'education.num']
drop
RandomForestClassifier(class_weight='balanced', random_state=123)
ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])['age', 'capital.gain', 'capital.loss', 'hours.per.week']
StandardScaler()
['education']
OrdinalEncoder(categories=[['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th',
'10th', '11th', '12th', 'HS-grad', 'Prof-school',
'Assoc-voc', 'Assoc-acdm', 'Some-college',
'Bachelors', 'Masters', 'Doctorate']],
dtype=<class 'int'>)['sex']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(drop='if_binary', dtype=<class 'int'>)
['workclass', 'marital.status', 'occupation', 'relationship', 'native.country']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
['fnlwgt', 'race', 'education.num']
drop
XGBClassifier(base_score=None, booster=None, callbacks=None,
colsample_bylevel=None, colsample_bynode=None,
colsample_bytree=None, device=None, early_stopping_rounds=None,
enable_categorical=False, eval_metric=None, feature_types=None,
gamma=None, grow_policy=None, importance_type=None,
interaction_constraints=None, learning_rate=None, max_bin=None,
max_cat_threshold=None, max_cat_to_onehot=None,
max_delta_step=None, max_depth=None, max_leaves=None,
min_child_weight=None, missing=nan, monotone_constraints=None,
multi_strategy=None, n_estimators=None, n_jobs=None,
num_parallel_tree=None, random_state=123, ...)ColumnTransformer(transformers=[('standardscaler', StandardScaler(),
['age', 'capital.gain', 'capital.loss',
'hours.per.week']),
('ordinalencoder',
OrdinalEncoder(categories=[['Preschool',
'1st-4th',
'5th-6th',
'7th-8th', '9th',
'10th', '11th',
'12th', 'HS-grad',
'Prof-school',
'Assoc-voc',
'Assoc-acdm',
'Some-college',
'Bachelors',
'Masters',
'Doctorate']],
dtype=<class...
OneHotEncoder(drop='if_binary',
dtype=<class 'int'>))]),
['sex']),
('pipeline-2',
Pipeline(steps=[('simpleimputer',
SimpleImputer(fill_value='missing',
strategy='constant')),
('onehotencoder',
OneHotEncoder(handle_unknown='ignore',
sparse_output=False))]),
['workclass', 'marital.status', 'occupation',
'relationship', 'native.country']),
('drop', 'drop',
['fnlwgt', 'race', 'education.num'])])['age', 'capital.gain', 'capital.loss', 'hours.per.week']
StandardScaler()
['education']
OrdinalEncoder(categories=[['Preschool', '1st-4th', '5th-6th', '7th-8th', '9th',
'10th', '11th', '12th', 'HS-grad', 'Prof-school',
'Assoc-voc', 'Assoc-acdm', 'Some-college',
'Bachelors', 'Masters', 'Doctorate']],
dtype=<class 'int'>)['sex']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(drop='if_binary', dtype=<class 'int'>)
['workclass', 'marital.status', 'occupation', 'relationship', 'native.country']
SimpleImputer(fill_value='missing', strategy='constant')
OneHotEncoder(handle_unknown='ignore', sparse_output=False)
['fnlwgt', 'race', 'education.num']
drop
LGBMClassifier(random_state=123, verbose=-1)
This VotingClassifier will take a vote using the predictions of the constituent classifier pipelines.
Main parameter: voting
voting='hard'it uses the output of
predictand actually votes.
voting='soft'with
voting='soft'it averages the output ofpredict_probaand then thresholds / takes the larger.
The choice depends on whether you trust
predict_probafrom your base classifiers - if so, it’s nice to access that information.
averaging_model.fit(X_train, y_train_num);
What happens when you
fitaVotingClassifier?It will fit all constituent models.
Note
It seems sklearn requires us to actually call fit on the VotingClassifier, instead of passing in pre-fit models. This is an implementation choice rather than a conceptual limitation.
Let’s look at particular test examples:
test_g50k = (
test_df.query("income == '>50K'")
.sample(4, random_state=42)
.drop(columns=["income"])
)
test_l50k = (
test_df.query("income == '<=50K'")
.sample(4, random_state=2)
.drop(columns=["income"])
)
averaging_model.classes_
array([0, 1])
What are the predictions given by the voting model?
data = {"y": 1, "Voting classifier": averaging_model.predict(test_g50k)}
pd.DataFrame(data)
| y | Voting classifier | |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
For hard voting, these are the votes:
r1 = {
name: classifier.predict(test_g50k)
for name, classifier in averaging_model.named_estimators_.items()
}
data.update(r1)
pd.DataFrame(data)
| y | Voting classifier | logistic regression | decision tree | random forest | XGBoost | LightGBM | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 2 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
For soft voting, these are the scores:
r2 = {
name: classifier.predict_proba(test_g50k)[:, 1]
for name, classifier in averaging_model.named_estimators_.items()
}
data.update(r2)
pd.DataFrame(data)
| y | Voting classifier | logistic regression | decision tree | random forest | XGBoost | LightGBM | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0.663425 | 1.0 | 0.760000 | 0.719056 | 0.685786 |
| 1 | 1 | 1 | 0.245338 | 1.0 | 0.678924 | 0.506023 | 0.463582 |
| 2 | 1 | 1 | 0.636401 | 0.5 | 0.621537 | 0.712402 | 0.665882 |
| 3 | 1 | 1 | 0.615662 | 0.0 | 0.770000 | 0.694334 | 0.683015 |
(Aside: the probability scores from DecisionTreeClassifier are pretty bad)
What’s the prediction probability of the averaging model? Let’s examine prediction probability of the first example from test_g50k.
averaging_model.predict_proba(test_g50k)[1]
array([0.42122672, 0.57877328])
It adds the prediction probabilities given by constituent models and divides the summation by the number of constituent models.
# Sum of probabilities for class 0 at index 1
sum_prob_ex1_class_0 = np.sum(
[
classifier.predict_proba(test_g50k)[1][0]
for name, classifier in averaging_model.named_estimators_.items()
]
)
sum_prob_ex1_class_0
2.1061336153264447
# Sum of probabilities for class 1 at index 1
sum_prob_ex1_class_1 = np.sum(
[
classifier.predict_proba(test_g50k)[1][1]
for name, classifier in averaging_model.named_estimators_.items()
]
)
sum_prob_ex1_class_1
2.8938663846735553
n_constituents = len(averaging_model.named_estimators_)
n_constituents
5
sum_prob_ex1_class_0 / n_constituents, sum_prob_ex1_class_1 / n_constituents
(0.42122672306528897, 0.578773276934711)
averaging_model.predict_proba(test_g50k)[1]
array([0.42122672, 0.57877328])
They match!
Let’s see how well this model performs.
averaging_model.predict_proba(test_g50k)[2]
array([0.37275576, 0.62724424])
results["Voting"] = mean_std_cross_val_scores(
averaging_model, X_train, y_train, return_train_score=True, scoring=scoring_metric
)
pd.DataFrame(results).T
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| Dummy | 0.014 (+/- 0.004) | 0.010 (+/- 0.001) | 0.758 (+/- 0.000) | 0.758 (+/- 0.000) |
| logistic regression | 0.470 (+/- 0.088) | 0.013 (+/- 0.001) | 0.849 (+/- 0.005) | 0.850 (+/- 0.001) |
| decision tree | 0.131 (+/- 0.007) | 0.012 (+/- 0.001) | 0.817 (+/- 0.006) | 0.979 (+/- 0.000) |
| random forest | 1.445 (+/- 0.025) | 0.077 (+/- 0.001) | 0.844 (+/- 0.007) | 0.976 (+/- 0.001) |
| XGBoost | 0.224 (+/- 0.021) | 0.016 (+/- 0.001) | 0.871 (+/- 0.005) | 0.899 (+/- 0.002) |
| LightGBM | 0.228 (+/- 0.064) | 0.026 (+/- 0.003) | 0.872 (+/- 0.004) | 0.888 (+/- 0.000) |
| CatBoost | 5.158 (+/- 0.037) | 0.211 (+/- 0.002) | 0.872 (+/- 0.003) | 0.895 (+/- 0.001) |
| sklearn_histGB | 0.904 (+/- 0.125) | 0.027 (+/- 0.002) | 0.871 (+/- 0.005) | 0.887 (+/- 0.002) |
| sklearn_GB | 2.084 (+/- 0.035) | 0.016 (+/- 0.001) | 0.864 (+/- 0.004) | 0.870 (+/- 0.001) |
| Voting | 2.475 (+/- 0.101) | 0.154 (+/- 0.004) | 0.859 (+/- 0.005) | 0.953 (+/- 0.001) |
It appears that here we didn’t do much better than our best classifier :(.
Let’s try removing decision tree classifier.
classifiers_ndt = classifiers.copy()
del classifiers_ndt["decision tree"]
averaging_model_ndt = VotingClassifier(
list(classifiers_ndt.items()), voting="soft"
) # need the list() here for cross_val to work!
results["Voting_ndt"] = mean_std_cross_val_scores(
averaging_model_ndt,
X_train,
y_train,
return_train_score=True,
scoring=scoring_metric,
)
pd.DataFrame(results).T
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| Dummy | 0.014 (+/- 0.004) | 0.010 (+/- 0.001) | 0.758 (+/- 0.000) | 0.758 (+/- 0.000) |
| logistic regression | 0.470 (+/- 0.088) | 0.013 (+/- 0.001) | 0.849 (+/- 0.005) | 0.850 (+/- 0.001) |
| decision tree | 0.131 (+/- 0.007) | 0.012 (+/- 0.001) | 0.817 (+/- 0.006) | 0.979 (+/- 0.000) |
| random forest | 1.445 (+/- 0.025) | 0.077 (+/- 0.001) | 0.844 (+/- 0.007) | 0.976 (+/- 0.001) |
| XGBoost | 0.224 (+/- 0.021) | 0.016 (+/- 0.001) | 0.871 (+/- 0.005) | 0.899 (+/- 0.002) |
| LightGBM | 0.228 (+/- 0.064) | 0.026 (+/- 0.003) | 0.872 (+/- 0.004) | 0.888 (+/- 0.000) |
| CatBoost | 5.158 (+/- 0.037) | 0.211 (+/- 0.002) | 0.872 (+/- 0.003) | 0.895 (+/- 0.001) |
| sklearn_histGB | 0.904 (+/- 0.125) | 0.027 (+/- 0.002) | 0.871 (+/- 0.005) | 0.887 (+/- 0.002) |
| sklearn_GB | 2.084 (+/- 0.035) | 0.016 (+/- 0.001) | 0.864 (+/- 0.004) | 0.870 (+/- 0.001) |
| Voting | 2.475 (+/- 0.101) | 0.154 (+/- 0.004) | 0.859 (+/- 0.005) | 0.953 (+/- 0.001) |
| Voting_ndt | 2.427 (+/- 0.137) | 0.142 (+/- 0.007) | 0.871 (+/- 0.005) | 0.918 (+/- 0.001) |
Still the averaging scores are not better than the best performing model.
It didn’t happen here but how could the average do better than the best model???
From the perspective of the best estimator (in this case CatBoost), why are you adding on worse estimators??
Here’s how this can work:
Example |
log reg |
rand forest |
cat boost |
Averaged model |
|---|---|---|---|---|
1 |
✅ |
✅ |
❌ |
✅✅❌=>✅ |
2 |
✅ |
❌ |
✅ |
✅❌✅=>✅ |
3 |
❌ |
✅ |
✅ |
❌✅✅=>✅ |
In short, as long as the different models make different mistakes, this can work.
Probably in our case, we didn’t have enough diversity.
Why not always do this?
fit/predicttime.Reduction in interpretability.
Reduction in code maintainability (e.g. Netflix prize).
What kind of estimators can we combine?#
You can combine
completely different estimators, or similar estimators.
estimators trained on different samples.
estimators with different hyperparameter values.
❓❓ Questions for you#
Is it possible to get better than the best performing model using averaging.
Is random forest an averaging model?
Stacking#
Another type of ensemble is stacking.
Instead of averaging the outputs of each estimator, use their outputs as inputs to another model.
By default for classification, it uses logistic regression.
We don’t need a complex model here necessarily, more of a weighted average.
The features going into the logistic regression are the classifier outputs, not the original features!
So the number of coefficients = the number of base estimators!
from sklearn.ensemble import StackingClassifier
The code starts to get too slow here; so we’ll keep CatBoost out.
stacking_model = StackingClassifier(list(classifiers.items()))
stacking_model.fit(X_train, y_train);
What’s going on in here?
It is doing cross-validation by itself by default (see documentation)
Note that estimators_ are fitted on the full X while final_estimator_ is trained using cross-validated predictions of the base estimators using cross_val_predict.
Here is the input features (X) to the meta-model:
valid_sample_df = train_df.sample(10, random_state=12)
valid_sample_X = valid_sample_df.drop(columns=["income"])
valid_sample_y = valid_sample_df['income']
# data = {}
# r4 = {
# name + "_proba": pipe.predict_proba(valid_sample_X)[:, 1]
# for (name, pipe) in stacking_model.named_estimators_.items()
# }
# data['y'] = valid_sample_y
# data.update(r4)
# pd.DataFrame(data)
Our meta-model is logistic regression (which it is by default).
Let’s look at the learned coefficients.
pd.DataFrame(
data=stacking_model.final_estimator_.coef_.flatten(),
index=classifiers.keys(),
columns=["Coefficient"],
).sort_values("Coefficient", ascending=False)
| Coefficient | |
|---|---|
| LightGBM | 4.060663 |
| XGBoost | 1.990023 |
| logistic regression | 0.689666 |
| random forest | 0.031574 |
| decision tree | -0.122754 |
stacking_model.final_estimator_.intercept_
array([-3.31973722])
It seems that the LightGBM is being trusted the most.
It’s funny that it has given a negative coefficient to decision tree.
Our meta model doesn’t trust decision tree model.
In fact, if the decision tree model says class >=50k, the model is likely to predict the opposite 🙃
stacking_model.predict(test_g50k)
array(['>50K', '<=50K', '>50K', '>50K'], dtype=object)
stacking_model.predict_proba(test_g50k)
array([[0.22188244, 0.77811756],
[0.58962301, 0.41037699],
[0.2316477 , 0.7683523 ],
[0.2168005 , 0.7831995 ]])
(This is the predict_proba from meta model logistic regression)
Let’s see how well this model performs.
results["Stacking"] = mean_std_cross_val_scores(
stacking_model, X_train, y_train, return_train_score=True, scoring=scoring_metric
)
pd.DataFrame(results).T
| fit_time | score_time | test_score | train_score | |
|---|---|---|---|---|
| Dummy | 0.014 (+/- 0.004) | 0.010 (+/- 0.001) | 0.758 (+/- 0.000) | 0.758 (+/- 0.000) |
| logistic regression | 0.470 (+/- 0.088) | 0.013 (+/- 0.001) | 0.849 (+/- 0.005) | 0.850 (+/- 0.001) |
| decision tree | 0.131 (+/- 0.007) | 0.012 (+/- 0.001) | 0.817 (+/- 0.006) | 0.979 (+/- 0.000) |
| random forest | 1.445 (+/- 0.025) | 0.077 (+/- 0.001) | 0.844 (+/- 0.007) | 0.976 (+/- 0.001) |
| XGBoost | 0.224 (+/- 0.021) | 0.016 (+/- 0.001) | 0.871 (+/- 0.005) | 0.899 (+/- 0.002) |
| LightGBM | 0.228 (+/- 0.064) | 0.026 (+/- 0.003) | 0.872 (+/- 0.004) | 0.888 (+/- 0.000) |
| CatBoost | 5.158 (+/- 0.037) | 0.211 (+/- 0.002) | 0.872 (+/- 0.003) | 0.895 (+/- 0.001) |
| sklearn_histGB | 0.904 (+/- 0.125) | 0.027 (+/- 0.002) | 0.871 (+/- 0.005) | 0.887 (+/- 0.002) |
| sklearn_GB | 2.084 (+/- 0.035) | 0.016 (+/- 0.001) | 0.864 (+/- 0.004) | 0.870 (+/- 0.001) |
| Voting | 2.475 (+/- 0.101) | 0.154 (+/- 0.004) | 0.859 (+/- 0.005) | 0.953 (+/- 0.001) |
| Voting_ndt | 2.427 (+/- 0.137) | 0.142 (+/- 0.007) | 0.871 (+/- 0.005) | 0.918 (+/- 0.001) |
| Stacking | 12.811 (+/- 0.298) | 0.158 (+/- 0.004) | 0.873 (+/- 0.004) | 0.890 (+/- 0.003) |
The situation here is a bit mind-boggling.
On each fold of cross-validation it is doing cross-validation.
This is really loops within loops within loops within loops…
We can also try a different final estimator:
Let’s
DecisionTreeClassifieras a final estimator.
stacking_model_tree = StackingClassifier(
list(classifiers.items()), final_estimator=DecisionTreeClassifier(max_depth=3)
)
The results might not be very good. But we can visualize the tree:
stacking_model_tree.fit(X_train, y_train);
custom_plot_tree(stacking_model_tree.final_estimator_,
feature_names=list(classifiers.keys()),
class_names=['"<=50K"', '">50K"'],
impurity=False,
fontsize=6)
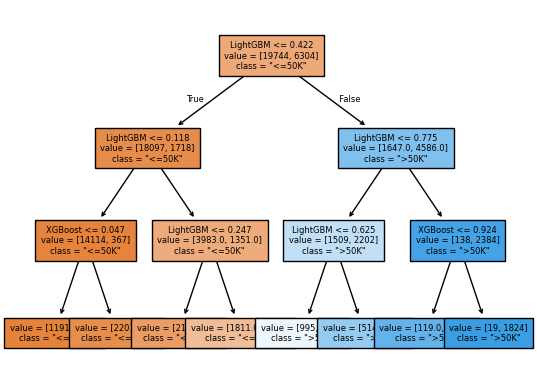
An effective strategy#
Randomly generate a bunch of models with different hyperparameter configurations, and then stack all the models.
What is an advantage of ensembling multiple models as opposed to just choosing one of them?
You may get a better score.
What is a disadvantage of ensembling multiple models as opposed to just choosing one of them?
Slower, more code maintenance issues.
There are equivalent regression models for all of these:
RandomForestClassifier\(\rightarrow\)RandomForestRegressorLGBMClassifier\(\rightarrow\)LGBMRegressorXGBClassifier\(\rightarrow\)XGBRegressorCatBoostClassifier\(\rightarrow\)CatBoostRegressorVotingClassifier\(\rightarrow\)VotingRegressorStackingClassifier\(\rightarrow\)StackingRegressor
Read documentation of each of these.
Summary#
You have a number of models in your toolbox now.
Ensembles are usually pretty effective.
Tree-based models are particularly popular and effective on a wide range of problems.
But they trade off code complexity and speed for prediction accuracy.
Don’t forget that hyperparameter optimization multiplies the slowness of the code!
Stacking is a bit slower than voting, but generally higher accuracy.
As a bonus, you get to see the coefficients for each base classifier.
All the above models have equivalent regression models.
Relevant papers#
Fernandez-Delgado et al. 2014 compared 179 classifiers on 121 datasets:
First best class of methods was Random Forest and second best class of methods was (RBF) SVMs.
If you like to read original papers here is the original paper on Random Forests by Leo Breiman.
XGBoost, LightGBM or CatBoost — which boosting algorithm should I use?
