Introduction to Recursion

Week 3, Wednesday

January 22, 2026

The 96 Days of DSCI 221

🎵 On the ninety-sixth day…

96 moments of zen 🎵 95 grateful neurons 🎵 94 clever insights 🎵 93 aha moments 🎵 92 merge conflicts 🎵 91 Stack Overflow tabs 🎵 90 refactored functions 🎵 89 git commits 🎵 88 test cases 🎵 87 rubber ducks 🎵 86 coffee refills 🎵 85 keyboard clicks 🎵 84 documentation pages 🎵 83 variable names 🎵 82 edge cases 🎵 81 print statements 🎵 80 whiteboard markers 🎵 79 Piazza posts 🎵 78 recursive calls 🎵 77 helper functions 🎵 76 code reviews 🎵 75 unit tests 🎵 74 bug fixes 🎵 73 loop iterations 🎵 72 hash collisions 🎵 71 array indices 🎵 70 base cases 🎵 69 pointer errors 🎵 68 syntax errors 🎵 67 runtime exceptions 🎵 66 stack frames 🎵 65 heap allocations 🎵 64 binary digits 🎵 63 terminal commands 🎵 62 Slack messages 🎵 61 Discord pings 🎵 60 Zoom breakouts 🎵 59 office hours 🎵 58 study sessions 🎵 57 flashcards 🎵 56 practice problems 🎵 55 lecture notes 🎵 54 code snippets 🎵 53 TODO comments 🎵 52 FIXME tags 🎵 51 deprecation warnings 🎵 50 linter errors 🎵 49 type hints 🎵 48 docstrings 🎵 47 assert statements 🎵 46 boundary checks 🎵 45 null pointers 🎵 44 empty lists 🎵 43 off-by-ones 🎵 42 infinite loops 🎵 41 segfaults 🎵 40 memory leaks 🎵 39 cache misses 🎵 38 race conditions 🎵 37 deadlocks 🎵 36 timeouts 🎵 35 snack breaks 🎵 34 memes shared 🎵 33 playlists made 🎵 32 naps attempted 🎵 31 alarms snoozed 🎵 30 tabs still open 🎵 29 unread emails 🎵 28 doodles drawn 🎵 27 songs on repeat 🎵 26 empty notebooks 🎵 25 highlighters 🎵 24 sticky notes 🎵 23 “almost dones” 🎵 22 existential crises 🎵 21 snacks consumed 🎵 20 walks taken 🎵 19 deep breaths 🎵 18 pokemons 🎵 17 demos 🎵 16 pull requests 🎵 15 code comments 🎵 14 merge commits 🎵 13 Piazza posts 🎵 12 cups of ramen 🎵 11 syntax errors 🎵 10 ChatGPT tabs 🎵 9 hours of sleep 🎵 8 TA office hours 🎵 7 Pomodoros 🎵 6 study rooms 🎵 5 passing tests 🎵 4 stretch breaks 🎵 3 docs read 🎵 2 good friends 🎵 And a latte from Loafe.

The Question

How many treats will you receive on the 96th day (Apr 10)?

\[1 + 2 + 3 + \ldots + 96 = \sum_{k=1}^{96} k = \text{ ?}\]

You’ve seen the closed form: \(\frac{n(n+1)}{2}\)

Proving the Closed Form

Claim: \(f(n) = \frac{n(n+1)}{2}\) where \(f(n) = \sum_{k=1}^{n} k\)

Proof: Consider an arbitrary \(n >= 0\). Then we have the following cases:

• Case 1, \(n = 0\) (base case): \(f(0) = 0 = \frac{0 \cdot 1}{2}\) ✓

• Case 2, \(n>0\) (inductive case):

Assume for any \(0 < j < n\), \(f(j) = \frac{j(j+1)}{2}\) (Inductive Hypothesis)

\(f(n) = f(n-1) + n\) by definition.

\(f(n-1) = \frac{(n-1)(n)}{2}\) by IH, since \(n-1 < n\).

\(f(n) = \frac{(n-1)(n)}{2} + n = \frac{(n)(n+1)}{2}\) by algebra. ✓

“Notice: the inductive step assumes f(k) works and uses it. Just like recursion!”

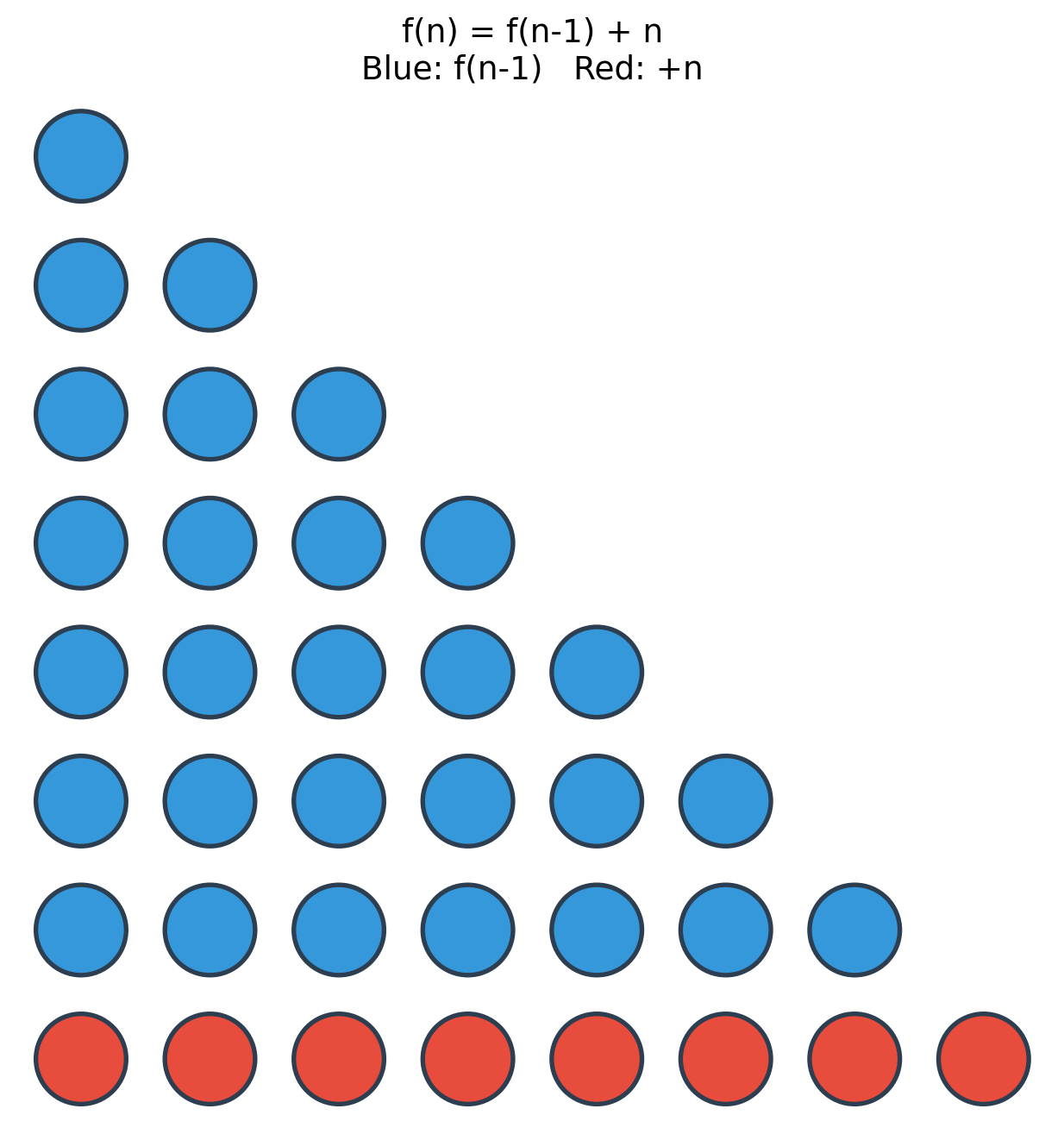
Recursive Thinking

The Recursive Structure: Peel Bottom Row

“The triangle with n rows = the triangle with n-1 rows + n more dots on the bottom.”

The Recursive Definition

A recursive mathematical function:

\[f(n) = \begin{cases} 0 & \text{if } n = 0 \\ f(n-1) + n & \text{if } n > 0 \end{cases}\]

“This is a recursive definition. The function is defined in terms of itself.”

Induction = Recursion

Induction	Math	Recursion
Consider arbitrary \(n \geq 0\)	\(n\in \mathbb{N}\)	def f(n):
Case \(n = 0\): prove directly	\(0\) if \(n=0\)	if n == 0: return 0
Case \(n > 0\): assume \(P(j)\) for \(j < n\)	\(f(n-1)\) defined	Trust f(n-1) works
Prove \(P(n)\) using IH	\(f(n-1)+n\) if \(n>0\)	Compute f(n) using f(n-1)

Same structure. Same reasoning.

“If you can prove it by induction, you can compute it by recursion. They’re the same thing.”

The Recursive Code

Consider the math:

\[f(n) = \begin{cases} 0 & \text{if } n = 0 \\ f(n-1) + n & \text{if } n > 0 \end{cases}\]

“The code is a direct translation of the math. Base case, recursive case.”

Intuition for Recursive Design

When you write triangle(n - 1), trust that it works.

This is exactly like relying on the inductive hypothesis in a proof.

Don’t trace through every call. Just ask:

1. Does my base case return the right thing?
2. If triangle(n-1) magically gives me the right answer, does my code use it correctly?

“The recursion fairy handles the recursive call. You just handle your level. Same as induction: assume P(k) holds, prove P(k+1).”

The Three Musts of Recursion

For the recursion to work its magic, your code must satisfy:

1. Handle all valid inputs: Every input needs a case (base or recursive)

2. Have a base case: At least one case that returns without recursing

3. Make progress: Each recursive call must get closer to a base case

“These are the contract with the recursion fairy. Break any of these, and your code will loop forever or crash.”

Same Triangle, Different View

What if we split the triangle differently?

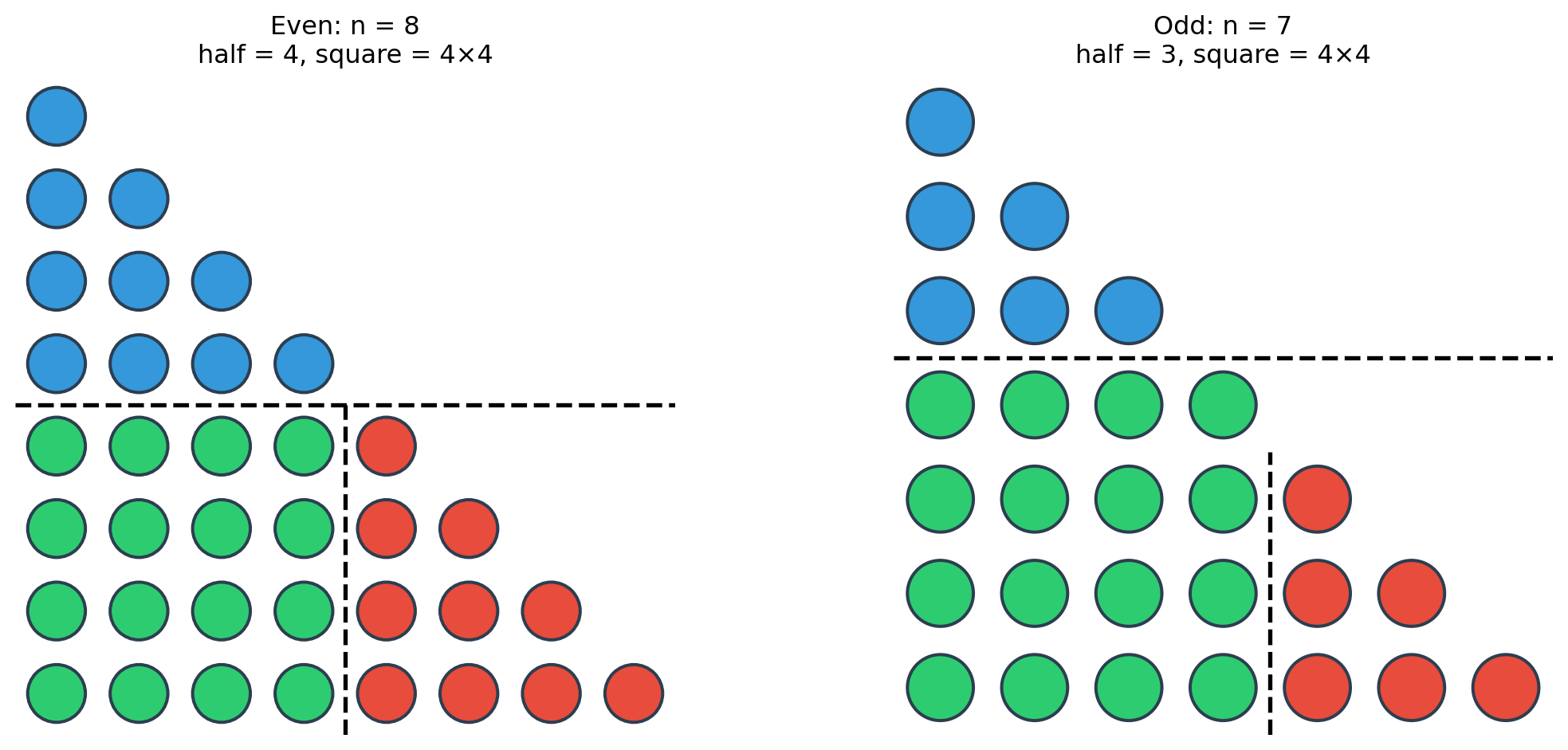
The Quadrant Decomposition

• Blue: Top triangle with \(\lfloor n/2 \rfloor\) rows → \(f(\lfloor n/2 \rfloor)\) dots
• Red: Bottom-right triangle with \(\lfloor n/2 \rfloor\) rows → \(f(\lfloor n/2 \rfloor)\) dots
• Green: Square of size \((n - \lfloor n/2 \rfloor)^2\) dots

\[f(n) = 2 \cdot f(\lfloor n/2 \rfloor) + (n - \lfloor n/2 \rfloor)^2\]

Works for all \(n\).

“Same problem, different recursive structure! The square absorbs the ‘extra’ row when n is odd.”

Two Functions, Same Answer

I forgot to define triangle_fast!

Which is Faster?

Both compute the same answer.

But the recursive structures are different:

• triangle(n): calls triangle(n-1)
• triangle_fast(n): calls triangle_fast(n//2)

Does that matter?

Let’s race them!

The Race

“Same answer. Wildly different performance. That’s the power of choosing the right decomposition.”

INSTRUCTOR NOTE (2026W2): After the race, go back and MODIFY triangle_fast to call triangle_fast(n//2) + triangle_fast(n//2) instead of 2 * triangle_fast(n//2). Race again. The “fast” version becomes SLOWER than the linear one! Students are amazed. This sets up the recurrence analysis in Week 4: T(n) = T(n/2) + O(1) vs T(n) = 2T(n/2) + O(1).

Why So Different?

triangle(n): \(f(n) = f(n-1) + n\)

• Recursion depth: \(n\)
• Total calls: \(n\)

triangle_fast(n): \(f(n) = 2 \cdot f(n/2) + (n/2)^2\)

• Recursion depth: \(\log_2(n)\)
• Total calls: \(\log_2(n)\)

“Linear depth vs logarithmic depth. At n=50000, that’s 50000 vs ~16.”

Big Idea: Recursion is About Decomposition

The same problem can have multiple recursive structures.

Different structures lead to different code and different performance.

This is the heart of algorithm design.

“This is why we study algorithms, not just ‘how to code’. The structure matters.”

What’s Next

• Lab 3: Writing recursive functions
• Week 4: Analyzing recursive running times (recurrences)
• Later: Divide-and-conquer algorithms (merge sort, quicksort)

The triangle race was a preview: smart decomposition → fast algorithms.

Summary

1. Recursion: A function defined in terms of itself
2. Base case: When to stop
3. Recursive case: How to reduce the problem
4. Key insight: The same problem can have different recursive structures
5. Performance: Structure choice affects speed dramatically

Questions?

INSTRUCTOR NOTE (2026W2): End the lecture with the “this was all non-sense” moment.

Ask: “This whole day has been non-sense. Why?”

Wait for responses: - Student: “We could have done this iteratively” → “Yes, but that would be essentially the same…” - Student: “We know the closed form!!” → BINGO!

Close with: “You could have written a function with NO recursion, NO iteration at all… just return n * (n + 1) // 2. Sometimes the best algorithm is no algorithm.”

This lands the punch that understanding the MATH lets you avoid computation entirely. Sets up the theme: data structures and algorithms are about being clever, not brute force.