Binary Search

Week 3, Tuesday (Video)

January 20, 2026

The Twenty Questions Puzzle

The Game

I’m thinking of a number between 0 and 63.

You can ask yes/no questions.

What’s your guaranteed winning strategy?

“How many questions do you need?”

How Many Questions?

Start with \(n = 64\) possibilities (0 to 63).

After each question: \(n \to n/2\)

Questions needed: \(\log_2(64) = 6\)

“6 questions for 64 possibilities. That’s the power of halving.”

Let’s Play!

I’m thinking of a number between 0 and 63.

You can ask yes/no questions.

Binary Search

The Problem

Given a sorted array and a target value, find the target’s index (or determine it’s not there).

0	1	2	3	4	5	6	7	8	9
2	5	8	12	16	23	38	56	72	91

Find target = 23.

“The array must be sorted. That’s the precondition.”

Linear Search: The Naive Approach

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

Worst case: \(\Theta(n)\)

“We might have to check every element.”

Binary Search: The Clever Approach

def binary_search(arr, target):
    lo, hi = 0, len(arr) - 1
    while lo <= hi:
        mid = (lo + hi) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            lo = mid + 1
        else:
            hi = mid - 1
    return -1

Worst case: \(\Theta(\log n)\)

“Each iteration halves the search space.”

Tracing Binary Search

0	1	2	3	4	5	6	7	8	9
2	5	8	12	16	23	38	56	72	91

Find target = 23:

1. lo=0, hi=9, mid=4 → arr[4]=16 < 23 → lo=5
2. lo=5, hi=9, mid=7 → arr[7]=56 > 23 → hi=6
3. lo=5, hi=6, mid=5 → arr[5]=23 ✓ → return 5

“Three comparisons instead of six. At scale, the difference is dramatic.”

The 17-Year Bug

“I’ve assigned binary search in courses at Bell Labs and IBM… and I’ve studied their solutions… In the history of this exercise, only about ten percent of professional programmers have gotten the program right.”

— Jon Bentley, Programming Pearls (1986)

The first correct binary search was published in 1946.

The first bug-free implementation? 1962.

“Even experts get it wrong. The loop invariant helps us get it right.”

Proving Binary Search Correct

The Invariant

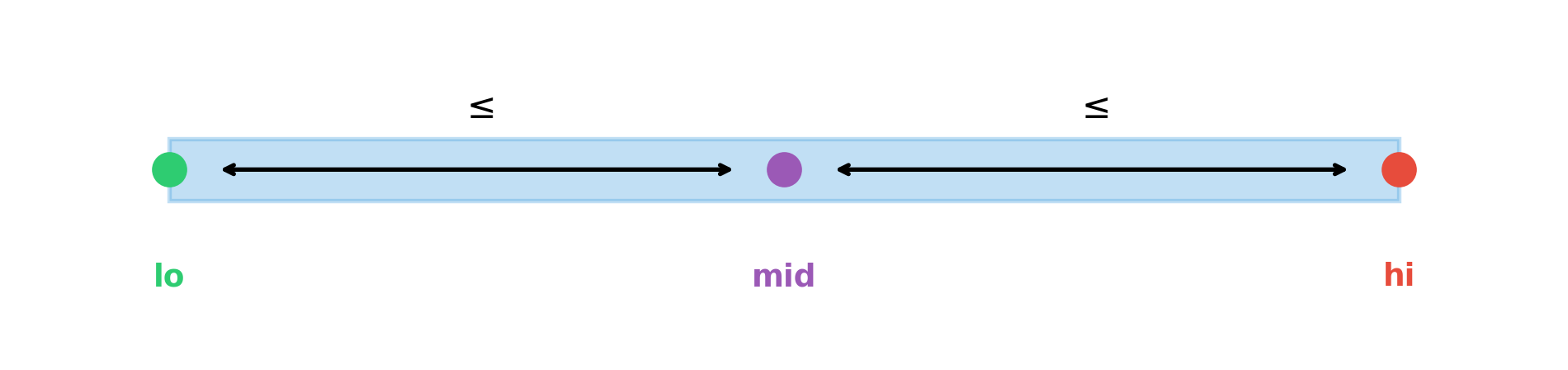
Invariant: If target is in arr, then target is in arr[lo:hi+1].

Equivalently: We haven’t excluded any index where target could be.

“This is the ‘search’ pattern: the answer is still in the remaining range.”

“The invariant holds at any point we might exit the loop.”

Base Case (Initialization)

Before the first iteration: lo = 0, hi = len(arr) - 1

arr[lo:hi+1] = arr[0:len(arr)] = entire array

If target is in arr, it’s in arr[lo:hi+1]. ✓

“We start with the full array. The invariant holds trivially.”

Key Fact: mid is Always Valid

Since lo <= hi (loop condition) and mid = (lo + hi) // 2:

\[\texttt{lo} \leq \texttt{mid} \leq \texttt{hi}\]

This means arr[mid] is always a valid access inside the loop.

“This is crucial for all three cases. We can safely access arr[mid] because mid is always in bounds.”

Inductive Step: Case 1 (Found it)

arr[mid] == target → we return mid.

Since lo <= mid <= hi, we know mid is in the search range.

We found the target and return its index. ✓

“Found it. The key fact tells us mid is valid, and we verified arr[mid] == target.”

Inductive Step: Case 2

arr[mid] < target

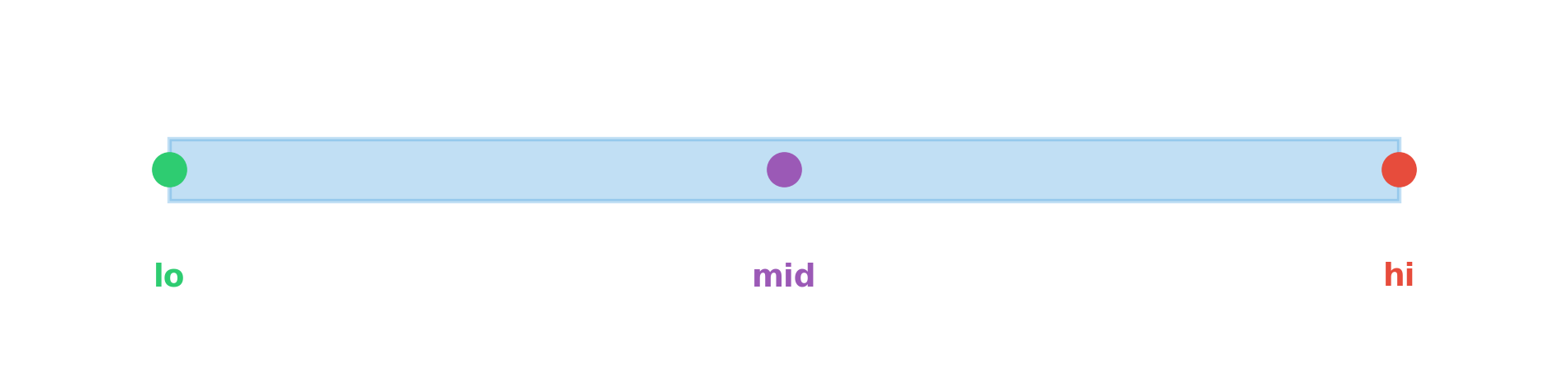
Setting lo = mid + 1 excludes only indices where target can’t be. ✓

“We’re safe to narrow the range because we’re only excluding impossible locations.”

Inductive Step: Case 3

arr[mid] > target

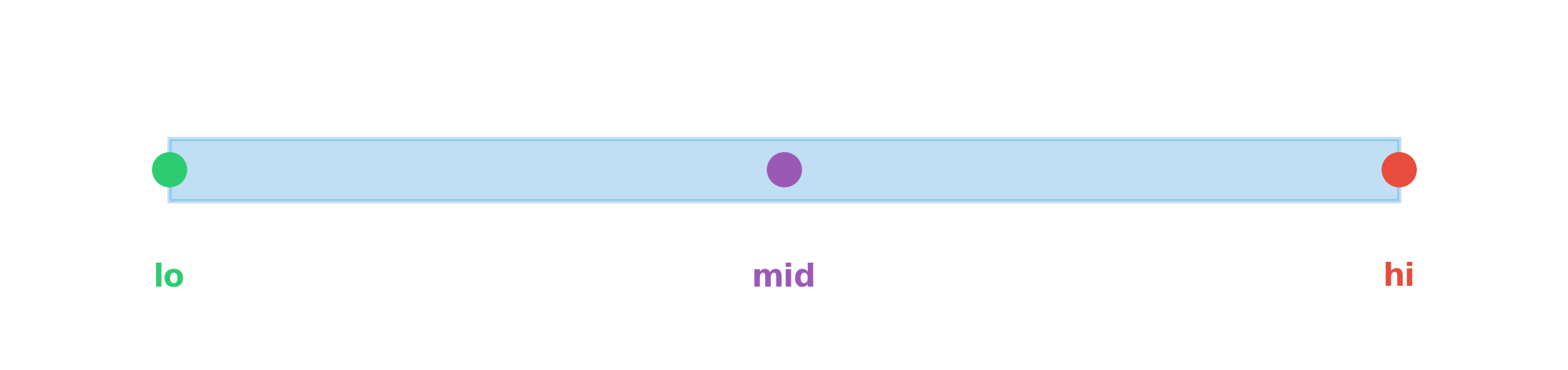
Setting hi = mid - 1 excludes only indices where target can’t be. ✓

“Same reasoning. We only narrow the range safely.”

Termination (Exit via lo > hi)

The loop exits when lo > hi.

At this exit point, arr[lo:hi+1] is empty.

The invariant says: if target is in arr, it’s in this empty range.

But nothing is in an empty range.

Therefore: target is not in arr. Return -1. ∎

“The invariant holds at this exit point too — it just tells us target isn’t there.”

The Proof in One Slide

Theorem: binary_search(arr, target) returns the index of target if present, else -1.

Proof: By induction on iteration count.

• Invariant: If target ∈ arr, then target ∈ arr[lo:hi+1]
• Base case: Initially, full array satisfies invariant ✓
• Inductive step: Each case either exits correctly or safely shrinks range ✓
• Termination: At exit, invariant \(\Rightarrow\) correct answer ∎

Why the Bug?

Common Mistakes

# Bug 1: Wrong comparison
while lo < hi:  # Should be lo <= hi
    ...

# Bug 2: Wrong update
lo = mid        # Should be mid + 1
hi = mid        # Should be mid - 1

# Bug 3: Integer overflow (in C/Java)
mid = (lo + hi) / 2  # Can overflow!
# Fix: mid = lo + (hi - lo) / 2

“Bug 1: misses the case where lo == hi. Bug 2: can cause infinite loop. Bug 3: famous Java bug, discovered in 2006 in Arrays.binarySearch!”

The Java Bug (2006)

// This was in java.util.Arrays for 9 years!
int mid = (low + high) / 2;  // OVERFLOW BUG

When low + high > Integer.MAX_VALUE, this overflows.

Fix:

int mid = low + (high - low) / 2;

“Joshua Bloch, who wrote the code, wrote about this bug. Even Google engineers get binary search wrong.”

The Invariant Saves You

When you’re unsure about an edge case, ask:

“Does this maintain the invariant?”

• lo = mid + 1: Does this exclude only impossible locations? Yes.
• hi = mid - 1: Does this exclude only impossible locations? Yes.
• lo <= hi: When does the search space become empty? When lo > hi.

“The invariant is your compass. When lost, check the invariant.”

Analysis

Worst-Case Running Time

Each iteration:

• Constant work (comparisons, arithmetic)
• Range shrinks by half: \((hi - lo + 1) \to \lfloor(hi - lo + 1)/2\rfloor\)

How many halvings until range is empty?

\(\log_2(n)\)

Worst case: \(\Theta(\log n)\)

“The halving is the key. That’s what gives us the logarithm.”

The Scale Comparison

\(n\)	Linear Search	Binary Search
1,000	1,000	10
1,000,000	1,000,000	20
1,000,000,000	1,000,000,000	30

“A billion elements, 30 comparisons. That’s the power of \(O(\log n)\).”

Racing Them

The Race

“Linear grows with n. Binary barely budges. That’s \(O(n)\) vs \(O(\log n)\).”

The Price of Speed

The Precondition

Binary search requires the array to be sorted.

What if it’s not sorted?

“Garbage in, garbage out. The invariant assumes sorted order.”

When to Use Binary Search

Use binary search when:

• Data is sorted (or can be sorted once, searched many times)
• Random access is \(O(1)\) (arrays, not linked lists)
• You need to find a specific value

Don’t use when:

• Data is unsorted and searched only once
• Data structure doesn’t support random access
• You need to find all occurrences

“Sorting costs \(O(n \log n)\). If you only search once, linear search wins.”

Summary

What We Learned

1. Binary search finds a target in \(\Theta(\log n)\) time (vs \(\Theta(n)\) for linear)

2. The invariant: “If target exists, it’s in arr[lo:hi+1]”

3. The proof: Init, Maintenance (3 cases), Termination

4. The bugs: Off-by-one errors, infinite loops, integer overflow

5. The precondition: Array must be sorted

Wednesday

Recursion: When the function calls itself.

• Thinking recursively
• Binary search, recursively
• The fractal coastline puzzle

“Binary search can also be written recursively. We’ll explore that Wednesday.”

Questions?

Binary search: \(\Theta(\log n)\)

The invariant makes it correct.

The halving makes it fast.