The Invariant Detective

Week 3, Monday

January 19, 2026

Warm-up: A Frozen Algorithm

The Scene

An algorithm was running, but we paused it mid-execution.

Your job: figure out what it was doing and where it stopped.

“Think of this like a crime scene investigation. The clues are in the state.”

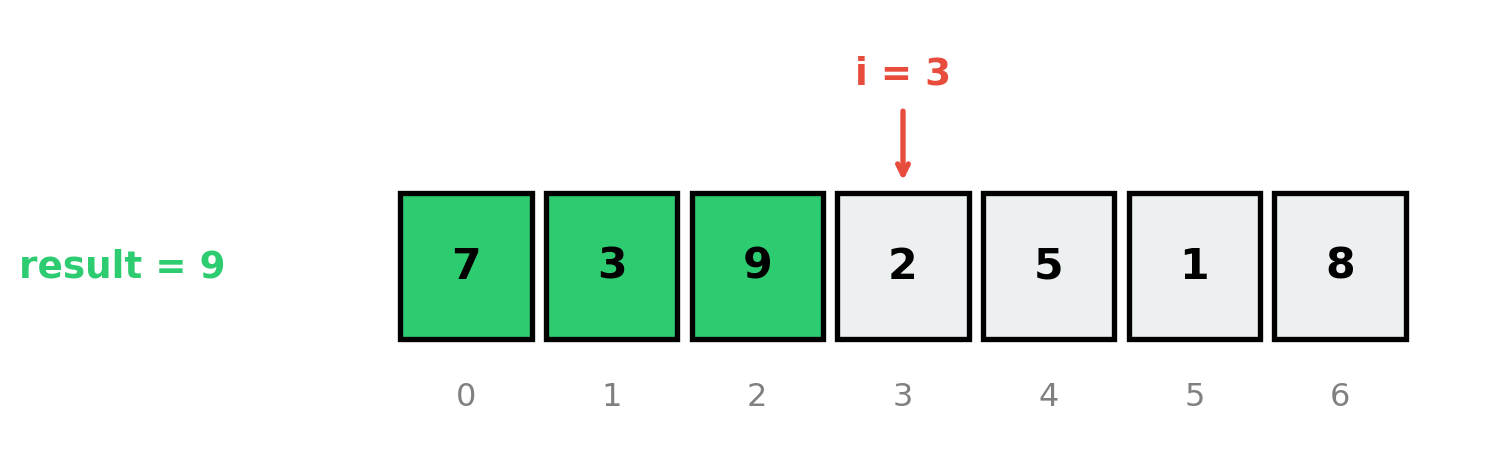
Puzzle 1: Find Maximum

Puzzle 1: Find Maximum

def mystery1(arr):
    result = arr[0]
    for i in range(1, len(arr)):
        if arr[i] > result:
            result = arr[i]
    return result

0	1	2	3	4	5	6
7	3	9	2	5	1	8

Variables: result = 9

Q1: What iteration is i about to start?

Q2: What does result represent?

“Pause and think. What value of i would give us result = 9?”

The Solution

• i = 3 (about to examine index 3)
• result = 9 = maximum of arr[0:3] = maximum of [7, 3, 9]

The Invariant: At iteration \(i\), result holds the maximum of arr[0:i].

Why This Works

The invariant tells us:

• At i = 1: result = max of arr[0:1] = max of [7] = 7 ✓
• At i = 2: result = max of arr[0:2] = max of [7, 3] = 7 ✓
• At i = 3: result = max of arr[0:3] = max of [7, 3, 9] = 9 ✓

The frozen state is consistent with the invariant at i = 3.

Puzzle 2: Counting

Puzzle 2: Counting

def mystery2(arr):
    count = 0
    for i in range(len(arr)):
        if arr[i] > 5:
            count += 1
    return count

0	1	2	3	4	5	6
4	8	2	7	1	9	3

Variables: count = 2

Q1: What iteration is i about to start?

Q2: State the invariant.

“Which elements > 5 have we seen? 8 at index 1, 7 at index 3. That’s 2 elements. So i = 4.”

The Solution

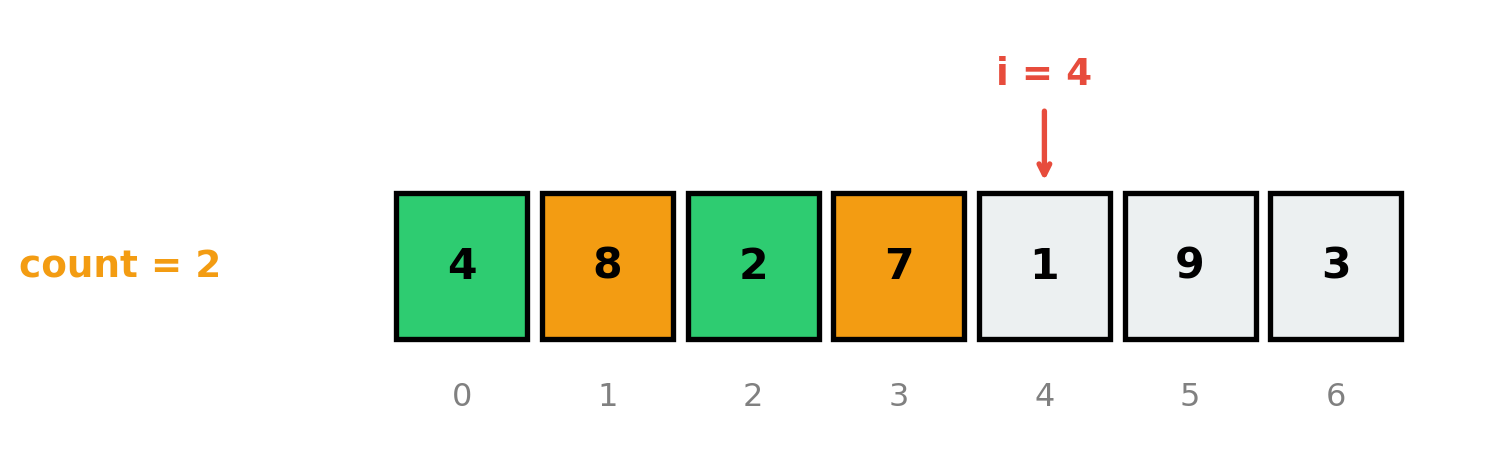
• Elements > 5 in arr[0:4] = [4, 8, 2, 7]: 8 and 7 → count = 2
• i = 4

The Invariant: At iteration \(i\), count equals the number of elements > 5 in arr[0:i].

Puzzle 3: Partitioning

Puzzle 3: Partitioning

def mystery3(arr):
    pivot = arr[0]
    left = 1
    for right in range(1, len(arr)):
        if arr[right] < pivot:
            arr[left], arr[right] = arr[right], arr[left]
            left += 1
    arr[0], arr[left - 1] = arr[left - 1], arr[0]
    return left - 1

Original: [5, 8, 2, 9, 1, 7, 3]

0	1	2	3	4	5	6
5	2	1	9	8	7	3

pivot = 5, left = 3

Q1: What iteration is right about to start?

Q2: Describe what’s in arr[1:left] and arr[left:right].

“This is trickier. Notice: arr[1:3] = [2, 1] — both < 5. arr[3:?] = ?”

The Visualization

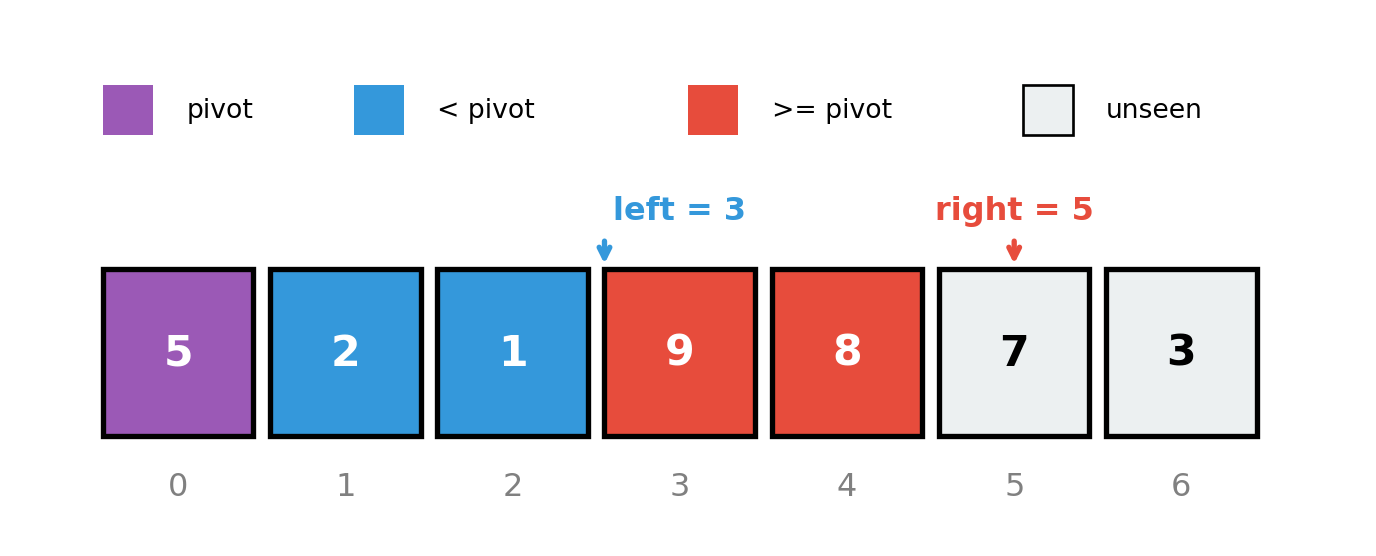
The Solution

• right = 5 (about to examine index 5, which has value 7)
• arr[1:left] = arr[1:3] = [2, 1] — all < pivot (5)
• arr[left:right] = arr[3:5] = [9, 8] — all >= pivot (5)

The Invariant (at iteration right):

• arr[1:left] contains elements < pivot
• arr[left:right] contains elements >= pivot
• arr[right:] is unexamined

“This is the partition step from quicksort! The invariant maintains two regions.”

The Detective Method

How to Find Invariants

1. Look at the loop variable: What does i (or right, etc.) represent?

2. Look at the accumulated state: What has result, count, left captured so far?

3. State the relationship: “At iteration \(i\), [variable] holds [property of arr[0:i]]”

4. Verify: Does the frozen state match your invariant?

Common Invariant Patterns

Pattern	Example Invariant
Accumulation	“total = sum of arr[0:i]”
Extremum	“max_val = maximum of arr[0:i]”
Counting	“count = number of X in arr[0:i]”
Search	“If target exists, it’s in arr[lo:hi+1]”
Partition	“arr[0:left] satisfies P, arr[left:i] doesn’t”

Practice: You Try

Puzzle 4

def mystery4(arr):
    total = 0
    for i in range(len(arr)):
        total += arr[i] * arr[i]
    return total

0	1	2	3	4	5	6	7
2	3	1	4	5	2	3	1

Variables: total = 14

Q1: What is i? Q2: State the invariant.

“Think: 2² + 3² + 1² = 4 + 9 + 1 = 14. So i = 3.”

Solution 4

\(2^2 + 3^2 + 1^2 = 4 + 9 + 1 = 14\)

So i = 3 (about to process index 3).

Invariant: At iteration \(i\), total = sum of squares of arr[0:i].

Puzzle 5

def mystery5(arr, target):
    lo, hi = 0, len(arr) - 1
    while lo <= hi:
        mid = (lo + hi) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            lo = mid + 1
        else:
            hi = mid - 1
    return -1

Frozen state: lo = 5, hi = 9, target = 72

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2	5	8	12	16	23	38	56	72	91	95	99	103	110	125	142

Q1: What just happened? Q2: State the invariant.

Solution 5

• We’re searching for 72
• lo = 5, hi = 9 means we’re looking in arr[5:10] = [23, 38, 56, 72, 91]
• Previous mid was 4 (value 16 < 72), so we set lo = 5

Invariant: If target is in arr, then target is in arr[lo:hi+1].

“We narrowed from the full array to indices 5-9. The invariant says: if 72 exists, it’s in this range. (And it is — at index 8.)”

Why This Matters

Debugging with Invariants

When your code doesn’t work:

1. State your invariant (what should be true?)
2. Print the state at each iteration
3. Find where the invariant breaks

The bug is where reality diverges from the invariant.

The Invariant as Compass

“When lost, check the invariant.”

• Unsure about an edge case? → Does it maintain the invariant?
• Code gives wrong answer? → Where does the invariant fail?
• Writing new code? → What invariant do I want to maintain?

Summary

What We Learned

1. Invariants are discoverable from frozen states

2. The pattern: “At iteration \(i\), [variable] holds [property of data seen so far]”

3. Common types: accumulation, extremum, counting, search range, partition

4. The detective method: Look at loop variable, look at accumulated state, state the relationship

Next Time

Recursion: When the function calls itself.

Spoiler: Recursion has invariants too — we call them recursive properties.