Discrete Math for Data Science

DSCI 220, 2025 W1

December 1, 2025

Announcements

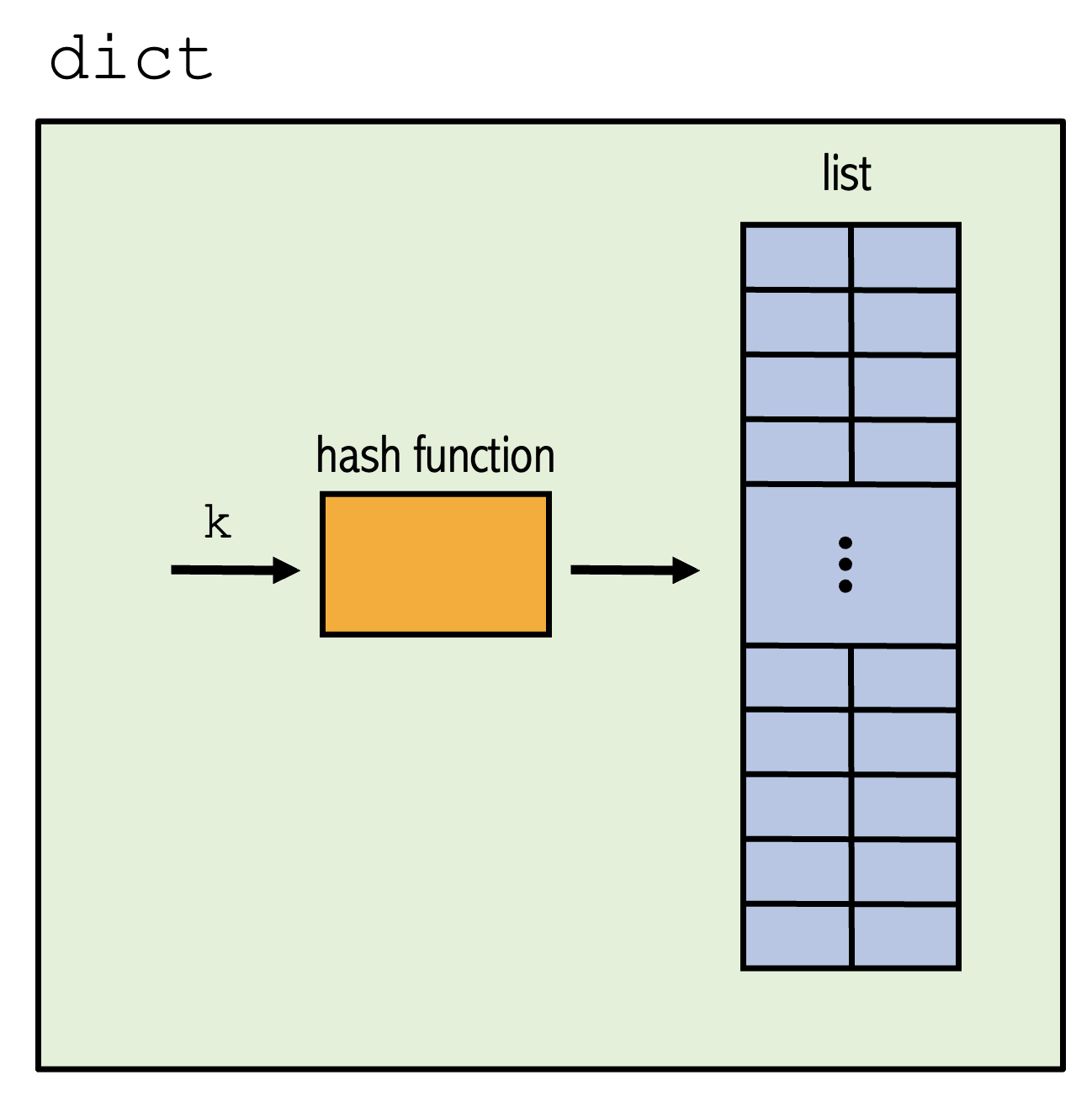
Hashing

Lists vs dictionaries

Suppose we want to store our friends’ favourite drink orders…

Use a list of pairs:

How do we find Bianca’s order?

Finding things with a list

If we store data in a list, to find Bianca’s order we have to search:

• Do you like this?
• What if the list were very long?
• What’s so special about the indices?

Python moment

Python has an implementation of an Associative Array called a dict.

Example Key: Value pairs

We often want to map one kind of thing (the key) to another kind of thing (the value):

• Song title → artist
  • "Anti-Hero" → "Taylor Swift"
• Course code → course title
  • "DSCI100" → "Intro to DSci"
• Email address → user ID
  • "alex@ubc.ca" → 1043921
• Date → temperature
  • "2025-11-27" → 9.3

• Flight → destination
  • "AC598" → SNA
• City name → population
  • "Vancouver" → 662248
• Word → number of times it appears
  • "hashing" → 17
• user ID → Email address
  • 1043921 → "alex@ubc.ca"

All of these are naturally modeled as key–value pairs — exactly what Python dictionaries (and hash tables) are built for.

Hashing

 

 

Where we are

• We’ve been thinking about functions:
  • \(f : X \to Y\)
  • “every \(x \in X\) gets exactly one \(y \in Y\)”
• We saw:
  • functions as sets of input–output pairs,
  • counting functions,
  • huge feature spaces (\(X\) can be enormous).

Today:

• A special and practical kind of function:
  • a hash function.
• Goal:
  • connect hashing to our function language,
  • introduce injective / surjective via a concrete example

Arrays vs associative arrays

A simple array/list:

• Indices: \(0,1,2,\dots,m-1\)
• Values: whatever we store there
• Access: by integer position, A[3]

An associative array:

• Keys: strings, IDs, course codes,
• Access: by key, T["DSCI220"]

Idea:

Use a function that turns a key into an index.

That function is called a hash function.

Recall: functions

Formal definition:

A function \(f : X \to Y\) assigns to each input \(x \in X\) exactly one output \(y \in Y\).

• \(X\) = domain
• \(Y\) = codomain

Today’s special case:

• \(X\) = set of keys (e.g., strings like "DSCI220")
• \(Y\) = set of indices \(\{0,1,\dots,m-1\}\)

So a hash function is just:

\[ h : \text{Keys} \to \{0,1,\dots,m-1\}. \]

Example

Let’s start with a set of keys:

• "MATH101", "DSCI220", "STAT201", "DSCI221"

And an array:

Goal: Define a hash function \(h\)

Observations

Notes:

• Every key has exactly one hash value. Why must this be true?
• No 2 keys share the same output.
• Every index is the output from some input.
• We call this a perfect hash function

Vocabulary: injective / surjective

Let \(f : X \to Y\).

• \(f\) is Injective (one-to-one) if:
  • \(x_1 \ne x_2\) implies \(f(x_1) \ne f(x_2)\).
  • No two different inputs share the same output.
• \(f\) is Surjective (onto) if:
  • For every \(y \in Y\), there is at least one \(x \in X\) with \(f(x) = y\).
  • Every output value is used.
• \(f\) is Bijective if:
  • it is both injective and surjective.
  • Perfect “pairing” between \(X\) and \(Y\).

On our 4 course codes and 4 buckets, \(h\) is bijective, a perfect hash for that key set.

Perfect hash functions

If we fix a finite set of keys \(K\):

• A function \(h : K \to \{0,\dots,m-1\}\) is a perfect hash for \(K\) if:
  • \(h\) is injective on \(K\) (no two keys collide),
  • so each key gets its own bucket.

If also \(|K| = m\) and \(h\) is surjective, then \(h\) is bijective on \(K\).

Perfect hash ⇒ no collisions (for that particular key set).

BUT:

• It might be very hand-crafted and fragile.
• It might stop being perfect as soon as we add more keys.

What if we add more keys?

• Keys: "MATH101", "DSCI220", "STAT201", "DSCI221", "DSCI100", "CPSC330", "STAT200"
• Buckets: \(\{0,1,2,3\}\) (4 buckets)
• Hash: \(h(\text{"*}xyz\text{"}) = (x+y+z) \bmod 4\)

Question:

1. We now have 7 keys and still 4 bucket. Can any function from these 7 keys to \(\{0,1,2,3\}\) be injective?
2. Why or why not?

Pigeonhole principle (PHP)

Formal version in our language:

• If \(|X| > |Y|\), then no function \(f : X \to Y\) can be injective.

Apply to hashing:

• Keys = pigeons
• Buckets = pigeonholes

If we have more keys than buckets:

• \[|\text{Keys}| > m = |\{0,\dots,m-1\}|,\]
• no hash function \(h : \text{Keys} \to \{0,\dots,m-1\}\) can be one-to-one on that key set.

Collisions

A collision happens when two different keys share the same hash value:

\[ k_1 \ne k_2, \quad h(k_1) = h(k_2). \]

By the pigeonhole principle:

• As soon as we have more keys than buckets,
  collisions are guaranteed (for every hash function).

A Rosey Hash Function

From “perfect” to “general-purpose”

We’ve seen: On a tiny, fixed set of keys, we can sometimes build a perfect hash

But for general-purpose hashing:

• The key space is HUGE (all possible strings, IDs, …), so we only ever see a sample of keys in our data.
• For any fixed hash function (h : {0,,m-1})…

Collisions before the table is full?

The pigeonhole principle told us:

• If the number of items actually stored in the table is greater than the number of buckets (m),
• then some bucket must contain at least 2 items.

So if we keep inserting more and more items while keeping (m) fixed, collisions are eventually guaranteed.

To ponder for next time:

• When we have fewer than (m) items, will we have collisions?