Discrete Math for Data Science

DSCI 220, 2025 W1

September 30, 2025

Announcements

Induction

Last Demo

This is a tromino:

This is a \(n\) by \(n\) deficient grid:

Claim: Every \(2^n\) by \(2^n\) deficient grid can be tiled with trominos.

Tile Work

Claim: Every \(2^n\) by \(2^n\) deficient grid can be tiled with trominos.

 

Proof: Line 1:

Line 2:

 

Small case(s):

Tile Work

Claim: Every \(2^n\) by \(2^n\) deficient grid can be tiled with trominos.

 

Proof continued… Inductive case:

Summations

Trick 5: Reindexing

 

Story. You only log every 3rd data point (rows 3, 6, 9, …).
The cost for row \(i\) is \(2i+1\).

Question. What is the total cost up to row \(n\)?

Trick 6: Double Sum

Story. Each item \(i\) must be compared with all later items \(j\ge i\). The pairwise cost is \(c_j = 4j+1\) (depends only on the later index).

Problem.
\(T = \displaystyle \sum_{i=1}^{n}\;\sum_{j=i}^{n}\,(4j+1)\)

Sequences

Hex Flowers

Consider the sequence of images below. How many cells are in image \(n\)? (Call it \(C_n\))

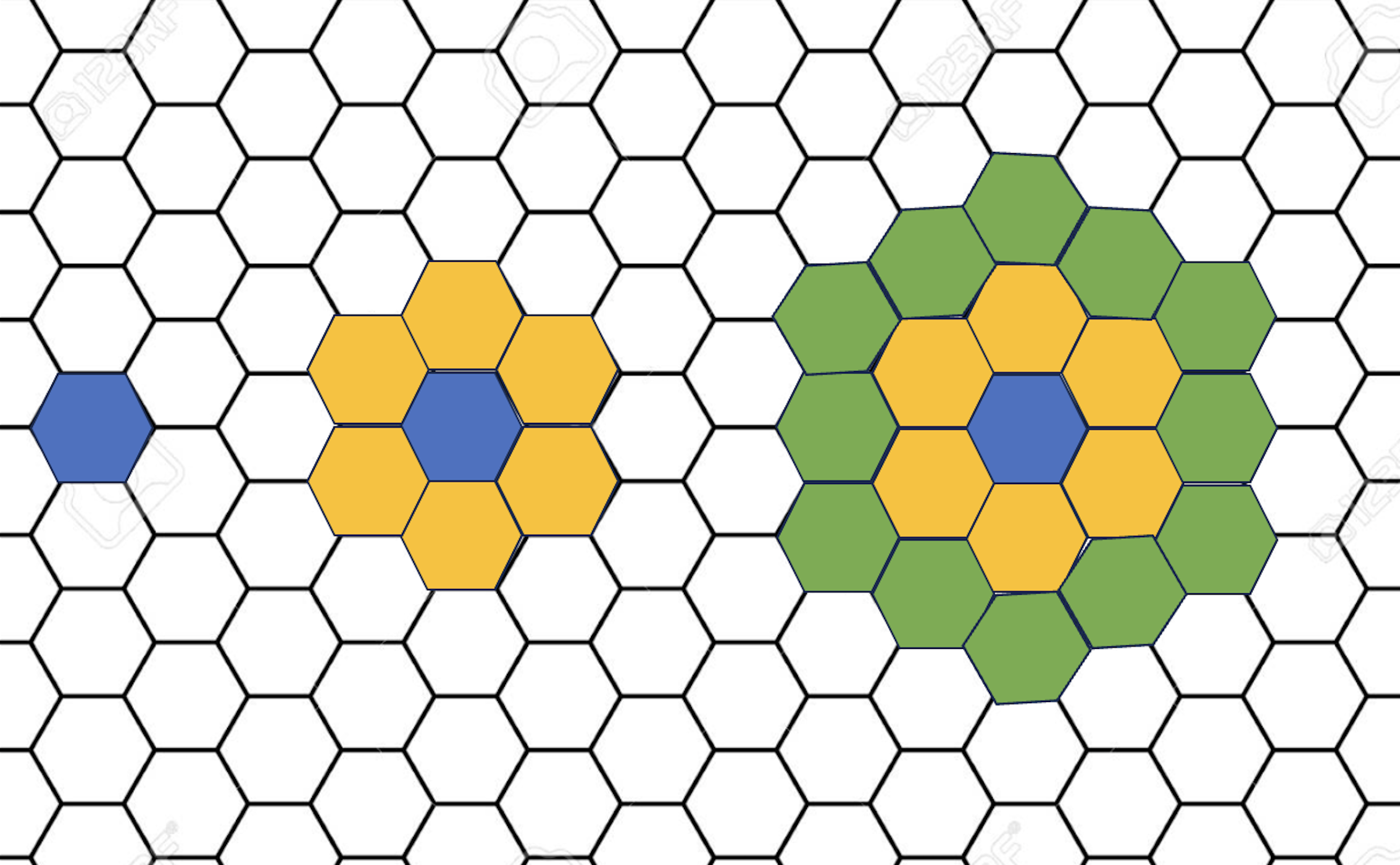
\(C_0 =\)

\(C_1 =\)

\(C_2 =\)

\(\ldots\)

\(C_n =\)

Hex Flowers

\(C_0 = 1\), and \(C_n = C_{n-1} + 6n, \forall n > 0\)

But what does this function mean? We need a closed form!!

Solving Recurrences

1. “unroll” the recurrence by substituting previous expressions.

2. See a pattern, and generalize it using \(k\).

3. Set the generalized term equal to the base case term.

4. Substitute base case and solve sums.

go back and put these numbers onto the solution

T

Consider the sequence of images below. How many dots are in image \(n\)? (Call it \(T_n\))

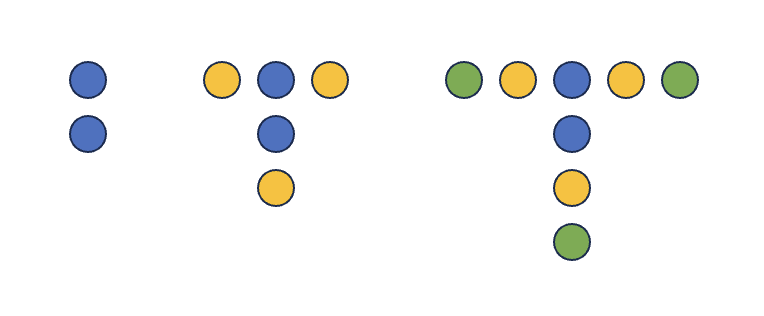
\(T_0 =\)

\(T_1 =\)

\(T_2 =\)

\(\ldots\)

\(T_n =\)

T

\(T_0 = 2\), and \(T_n = T_{n-1} + 3, \forall n > 0\)

But what does this function mean? We need a closed form!!

T

But how can we be sure our closed form is correct?

Claim: The closed form solution to the recurrence \(T_0 = 2\) and \(T_n = T_{n-1} + 3, \forall n > 0\) is \(T_n = 2 + 3n\)

Consider an arbitrary \(n\) and the given recurrence.

IH: Assume \(\forall j < n, T_j = 2 + 3j\).

Note that either \(n = 0\) (base case) or \(n > 0\) inductive case.

Case 1: \((n=0)\) The recurrence gives \(T_0 = 2\), and the closed form gives \(T_0 = 3\cdot 0 + 2 = 2\)

Case 2: \((n > 0)\) The recurrence gives \(T_n = T_{n-1} + 3\). But from the IH, we know \(T_{n-1} = 3(n-1) + 2\). We substitute to get \(T_n= [3(n-1) + 2] + 3 = 3n+2\).

Toothpicks

How many toothpicks in an \(n\cross n\) grid made of toothpicks?

Draw the sequence:

 

Find the recurrence:

 

Solve the closed form for the recurrence:

Buds