Discrete Math for Data Science
DSCI 220, 2025 W1
September 23, 2025
Announcements
Proofs
Today’s goals
- Recognize the form of common proof techniques \(\to\), \(\leftrightsquigarrow\), \(\bot\), ⊞
- Write short proofs using \(\bot\), and ⊞.
What is a proof?
A clear, finite chain of statements that:
- starts from assumptions/definitions
- uses valid rules
- ends with the claim
We’ll practice four approaches for \(P\to Q\) (first 2 earlier, second 2 now):
- \(\to\) Direct: assume the hypothesis, derive the conclusion
- \(\leftrightsquigarrow\) Contrapositive: prove \(\neg Q\to\neg P\) instead of \(P\to Q\)
- \(\bot\) Contradiction: assume \(P\) and \(\neg Q\); reach False
- ⊞ Cases: split into exhaustive cases; prove \(Q\) for each
Warm Up 1
Claim: for all integers \(a\) and \(b\), if \((a+b)\) is odd, then \(a\) is odd or \(b\) is odd.
- \(\to\) or \(\leftrightsquigarrow\)?
- Proof: Consider…
Warm Up 2
Claim: for all integers \(a\), if \(a^2\) is even, then \(a\) is even.
- \(\to\) or \(\leftrightsquigarrow\)?
- Proof: Consider…
Proof Skeleton Cards
\(\to\) Direct Proof of \(P\to Q\)
- Assume \(P\).
- Reason – Unpack definitions / apply given rules to derive needed facts from \(P\).
- … Therefore \(Q\).
\(\leftrightsquigarrow\) Contrapositive Proof of \(P\to Q\)
- Assume \(\neg Q\)
- Use rules/definitions that match \(\neg Q\) to drive toward \(\neg P\).
- … Therefore \(\neg Q\to\neg P\), and thus \(P\to Q\).
\(\bot\) Contradiction Proof of \(P\to Q\)
- Assume \(P\) and \(\neg Q\).
- Reason – Unpack definitions / apply given rules to derive needed facts from \(P\land \neg Q\), watch for contradiction (\(a\land\neg a\)).
- … Therefore \(\bot\), and our assumption of \(\neg Q\) must be false, so \(P\to Q\).
⊞ Cases Proof of \(P\to Q\)
- Partition \(P\) into cases \(P_1\), \(P_2\), etc. covering all possibilities.
- For each \(P_k\), show that \(P_k\to Q\).
- … Therefore, in each case \(Q\), and \(P\to Q\).
\(\bot\) Example Contradiction
Prove that any solution to the mini sudoku puzzle below must contain a 3 in the top right corner (r1c4).
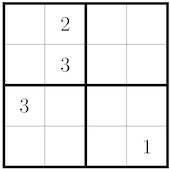
\(\bot\) Our Turn Contradiction
Claim: \(\sqrt 2\) is irrational.
Proof: (CLASSIC) Suppose by way of contradiction that \(\sqrt 2\) is rational. Then…
⊞ Example Cases
Claim: \(n^3 - n\) is divisible by ___.
Overview:
⊞ Proof Part 1 (Divisible by ___):
Consider an arbitrary \(n\). Then one of the following must be true
- Case A: \(n=3k\)
- Case B: \(n=3k+1\)
- Case C: \(n=3k+2\)
In all 3 cases, \(n^3-n\) is divisible by ___.
⊞ Proof Part 2 (Divisible by ___):
Consider an arbitrary \(n\). Then one of the following must be true
- Case A: \(n=2k\)
- Case B: \(n=2k+1\)
In all 2 cases, \(n^3-n\) is divisible by ___.
Conclusion: 2 and 3 are factors of \(n^3-n\) so 6 must be a factor!