Discrete Math for Data Science
DSCI 220, 2025 W1
September 22, 2025
Announcements
Reasoning
Explore UBC
Variable Definitions
- \(A\): Clock Tower is lit up
- \(B\): Nest is alight
- \(C\): Koerner Library is illuminated
- \(E\): ICCS doors are unlocked
- \(F\): the Gallery is open
- \(D\): Main Mall is hopping!
Rulebook
- \((A\lor B\lor C)\) — At least one of the three landmarks is lit tonight.
- \(A\to E\) — If Clock Tower is lit then ICCS is unlocked.
- \(C\to E\) — If Koerner is lit then ICCS is unlocked.
- \((B\lor F)\) — Either the Nest is lit, or the Gallery opens.
- \((E\land F)\to D\) — If ICCS unlocked and Gal opens then Mall hops.
- \(B\to D\) — If the Nest is lit then Mall hops.
Goal: Does \(D\) follow from the rulebook?
Answer: yes, using unit propagation, as illustrated by table activity.
today’s python
Does this always work?
Works great for: rulebooks where each clause has only 1 positive unit (Horn)
Can stall on: non-Horn, symmetric choice, more complex domains.
Stalling example: \[ (A\vee B)\wedge(A\vee \neg B)\wedge(\neg A\vee B)\wedge(\neg A\vee \neg B) \]
- No unit clauses → our method can’t start.
- It’s actually unsatisfiable but needs a branch to detect. (try \(A\) or \(\neg A\))
Takeaway 1: Propagation finds what’s locally forced.
When nothing is locally forced, we need case splits or stronger rules.
Takeaway 2: The general problem of boolean function “Satisfiability” (SAT) has no known efficient solution, and is a classic “NP-Complete” problem.
Proofs
Today’s goals
- Recognize the form of common proof techniques \(\to\), \(\leftrightsquigarrow\), \(\bot\), ⊞
- Write short proofs using \(\to\), and \(\leftrightsquigarrow\).
What is a proof?
A clear, finite chain of statements that:
- starts from assumptions/definitions
- uses valid rules
- ends with the claim
We’ll practice four approaches for \(P\to Q\) (first 2 today, second 2 on video lesson):
- \(\to\) Direct: assume the hypothesis, derive the conclusion
- \(\leftrightsquigarrow\) Contrapositive: prove \(\neg Q\to\neg P\) instead of \(P\to Q\)
- \(\bot\) Contradiction: assume \(P\) and \(\neg Q\); reach False
- ⊞ Cases: split into exhaustive cases; prove \(Q\) for each
Warm Up
Solve the Sudoku on the worksheet.
Speculate on an interesting feature of the corners.
Do all 4x4 Sudoku puzzles have this feature?
05:00
First Proof
Theorem: For any integers \(a\) and \(b\), if \(ab\) is even, then \(a\) is even or \(b\) is even.
Important definition:
Technical Rewrite
\(\forall a,b\in \mathbb{Z}\)
\(( (\exists k\in\mathbb{Z}, ab=2k) \to ((\exists j\in\mathbb{Z}, a = 2j) \lor (\exists j\in\mathbb{Z}, b=2j)))\)
Universal instantiation:
Which are valid arguments?
Pf1: Suppose \(a\) and \(b\) are odd. Then there are integers \(k\) and \(j\) so \(a=2k+1\) and \(b=2j+1\). Then \(ab=(2k+1)(2j+1) = 2(2jk + j + k) +1\). Since \(2jk+j+k\) is an integer, \(ab\) is odd.
Pf2: Assume \(a\) or \(b\) is even. Suppose \(a\) is even – the argument is the same if it is \(b\). Then \(ab=2kb\) for some \(k\), and thus \(ab\) is even.
Pf3: Suppose that \(ab\) is even but \(a\) and \(b\) are both odd. Namely, \(ab=2n\), \(a=2k+1\), and \(b=2j+1\), for some integers \(n\), \(j\), and \(k\). Then \(2n=(2k+1)(2j+1)\) and \(n = 2jk + k + j + 1/2\) which is a contradiction.
Pf4: Let \(ab\) be an even number, say \(ab=2n\), and \(a\) be an odd number, say \(a=2k+1\). Then \(2n = (2k+1)b\) and thus \(b=2(n-kb)\) and \(b\) is even.
Proof Skeleton Cards
\(\to\) Direct Proof of \(P\to Q\)
- Assume \(P\).
- Reason – Unpack definitions / apply given rules to derive needed facts from \(P\).
- … Therefore \(Q\).
\(\leftrightsquigarrow\) Contrapositive Proof of \(P\to Q\)
- Assume \(\neg Q\)
- Use rules/definitions that match \(\neg Q\) to drive toward \(\neg P\).
- … Therefore \(\neg Q\to\neg P\), and thus \(P\to Q\).
\(\bot\) Contradiction Proof of \(P\to Q\)
- Assume \(P\) and \(\neg Q\).
- Reason – Unpack definitions / apply given rules to derive needed facts from \(P\land \neg Q\), watch for contradiction (\(a\land\neg a\)).
- … Therefore \(\bot\), and our assumption of \(\neg Q\) must be false, so \(P\to Q\).
⊞ Cases Proof of \(P\to Q\)
- Partition \(P\) into cases \(P_1\), \(P_2\), etc. covering all possibilities.
- For each \(P_k\), show that \(P_k\to Q\).
- … Therefore, in each case \(Q\), and \(P\to Q\).
\(\to\) Example Direct
Prove that for any solution to the mini sudoku puzzle below, if the solution has a 2 in the top-left square (r1c1), then it will contain a 2 in the bottom-right square (r4c4).
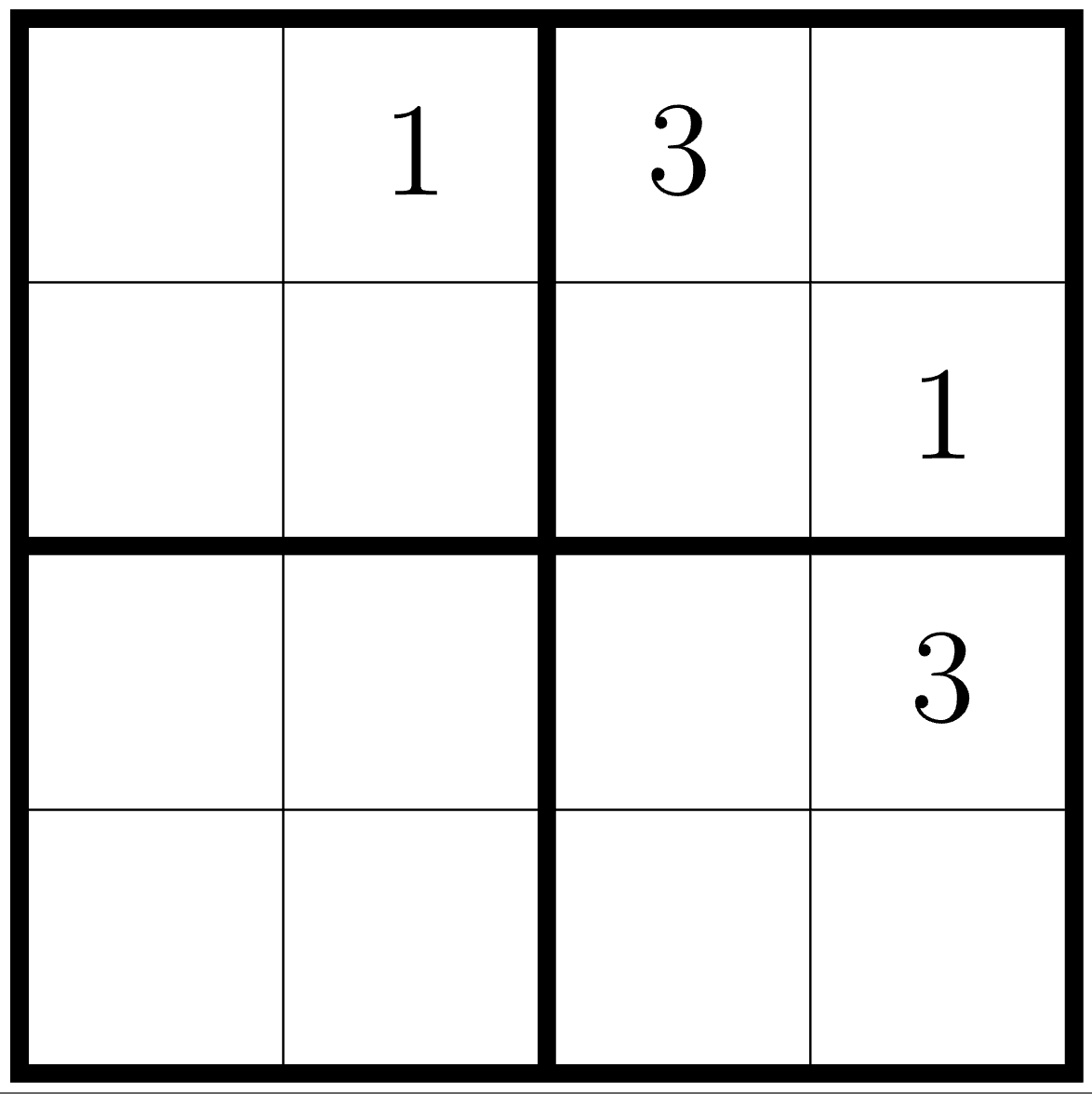
\(\to\) Your Turn Direct
Let \(T_n = \frac{n(n+1)}{2}\) be the \(n\)th triangular number, \(T_1=1\), \(T_2=3\), etc.
A glow number is any integer that can be written as the sum of two consecutive triangular numbers:
\[𝑔=𝑇_𝑘+𝑇_{𝑘+1}\] Theorem: every glow number is a perfect square.
Proof: Consider an arbitrary glow number \(g\).
… therefore \(g\) is a perfect square.
is the converse true?
\(\leftrightsquigarrow\) Example Contrapositive

Game rule: each 2x2 box contains one of 1, 2, 3, and 4.
Theorem: For any valid Sudoku solution, if A and B and C are not 4, then D is 4.
Contrapositive:
\(\leftrightsquigarrow\) Your Turn Contrapositive
Definitions:
- A number \(n\) is even if there is an integer \(k\) such that \(n=2k\).
- A number \(n\) is odd if there is an integer \(k\) such that \(n=2k+1\).
Theorem: If \(3n+2\) is odd, then \(n\) is odd.