Discrete Math for Data Science

DSCI 220, 2025 W1

September 10, 2025

Announcements

• Enroll in PrairieTest here: https://us.prairietest.com/pt/student/course/12361/enroll/392674810508
• Sign up for EX1. Practice materials (on PL) coming soon!
• We will have class THIS friday, but not thereafter.
• Tutorials begin next week.

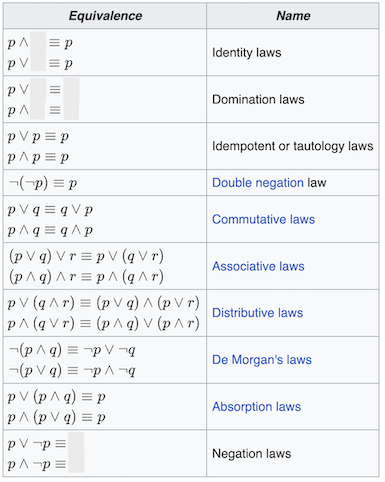
Logical Equivalences

Logical Equivalences

We have discussed Logical Equivalence (LE) and explored an example. The table illustrates LE that are so important, they have names!

Observations:

Logical Equivalence Practice

All graded learning activities in the course will use PrairieLearn.

Navigate to Activity 1 and complete question 2. Each of you will receive a different version of the problem. Work together in pairs to solve each person’s version.

https://us.prairielearn.com/pl/course_instance/186238/assessment/2562335

07:00

Implication

Implication

Connect operator \(\rightarrow\) to a logically equivalent expression using only and, or, and not.

\(p\)	\(q\)	\(p\rightarrow q\)	\(\underline{\hspace{3em}}\)
F	F	T
F	T	T
T	F	F
T	T	T

• Is this operator commutative?

• Note: \(p \rightarrow q \equiv\) _______.

• \(p \rightarrow q\) Corresponds to “if \(p\) then \(q\)”

• We’re not promising causation, only a truth condition.

• \(p \rightarrow q\) is False only when \(p\) is True and \(q\) is False.

• Gives us mechanism for reasoning (next week)!

q and not p is false. so it’s NOT (q^-p) == ??? (apply demorgan)

PL exercises on Logical equivalence involving implication?

More on implication and logical equivalence in tutorial questions

Suppose \(p\equiv\) T . Then \(p\) is a Tautology.

Suppose \(p\equiv\) F . Then \(p\) is a Contradiction.

Logical Equivalence Proof

Prove that \(p \rightarrow q \equiv \neg q \rightarrow \neg p\):

Vocabulary

Given \(p\rightarrow q\), we define the following 3 terms:

• ________________ is \(\neg q\rightarrow \neg p\)

• ________________ is \(q\rightarrow p\)

• ________________ is \(\neg p\rightarrow \neg q\)

Describe all the logical equivalences among the 4 statements:

we’ll see if English can help us!

Converses — check what’s True

#	Statement p→q	p→q	q→p
1	To be empty, a string must have length 0.	☐	☐
2	Playing in the NHL entails being a professional hockey player.	☐	☐
3	If an animal is a mammal, then it is a cat.	☐	☐
4	Riding the 99 B-Line counts as public transit.	☐	☐
5	If a dish is spicy, then it is Indian cuisine.	☐	☐
6	If it’s a kitten, then it’s a cat.	☐	☐
7	No song appears on the Billboard Hot 100 without reaching #1.	☐	☐
8	If I live in Totem Park residence, then I live in campus housing.	☐	☐
9	If I eat breakfast, then I ace the quiz.	☐	☐
10	If a movie is a superhero film, then it is an MCU movie.	☐	☐
11	If I’m an only child, then I have zero siblings.	☐	☐
12	If I’m in British Columbia, then I’m in Vancouver.	☐	☐

Biconditionals

We have a special operator for those implications whose converses are also True:

  \((p\rightarrow q) \wedge (q\rightarrow p)\equiv p\leftrightarrow q\)

Some phrases describing this relationship:

• biconditional
• if and only if (iff)
• equivalent

Which of the expressions on the previous page are biconditionals?

Words and Ideas

Logical Equivalence

Implication