Discrete Math for Data Science

DSCI 220, 2025 W1

September 8, 2025

Propositions Continued

WFFs

Rand WFF Apply rule on line:

Rand atom Atom becomes:

<wff> ::= <atom>
        | ~ <wff>
        | ( <wff> ∧ <wff> )
        | ( <wff> ∨ <wff> )

<atom> ::= p | q 

Example derivation:

<wff>

WFFs (Notes)

<wff> ::= <atom>
        | ~ <wff>
        | ( <wff> ∧ <wff> )
        | ( <wff> ∨ <wff> )

<atom> ::= p | q 

• Grammars can be used to construct many different kinds of sequences.

• We could have included additional operators \(\rightarrow\), \(\leftrightarrow\), \(\oplus\), \(\uparrow\)

• Computational evaluation of <wff>is covered in DSCI221. For now, we trust Python and focus on logic.

• The <wff> are propositions.

WFF Puzzle

Which of these are WFFs?

<wff> ::= <atom>
        | ~ <wff>
        | ( <wff> ∧ <wff> )
        | ( <wff> ∨ <wff> )

<atom> ::= p | q 

1. \((\neg p ∧ (q ∨ r))\)
2. \(((p ∧ q) ∨ (r ∧ \neg s))\)
3. \(((\neg p) ∨ (q ∨ r))\)

4. \((p ∨ (qr))\)
5. \(\neg (p ∨ (q ∧ \neg r))\)
6. \(\neg (p ∨ q))\)

03:00

Sometimes pq is the same as p^q, p & q, p && q, but our grammar only uses ^. In this course we will vary symbols fluidly, partly because we’re assembling info from many different sources, but also partly because you’ll need to be agile in the future. Note that the same issues exist for other operators.

WFFs

<wff> ::= <atom>
        | ~ <wff>
        | ( <wff> ∧ <wff> )
        | ( <wff> ∨ <wff> )

<atom> ::= p | q 

Theorem: \(\neg (p ∨ q))\) is not a WFF.

Proof:

assume that it is! then ~ must have been the last rule applied, and \(( p v q))\) must be a . then ( v ) must have been the last rule applied, and \(p\) and \(q)\) must be . take each case separately: \(q)\) is not a because none of the rules apply, so we have both that it must be a wff and it is not a wff – a contradiction, so our assumption is false!

We include this as foreshadowing for a proof strategy called “proof by contradition.” Making arguments like this (proofs) is the substance of this course, but don’t worry, we’ll be teaching you how to do it.

Back to Propositions

A proposition is a statement that can be either True or False.

Examples:

• \(37 > 12\)

• Fewer than 5 people in this room feel sleepy.

• There are extra-terrestrial life forms.

• This statement is False.

• \(\underline{\hspace{10em}}\)

Translation

From English to logic and back…

\(p\): ___________ ate cereal for breakfast.

\(q\): ___________ brought a backpack to class.

 

• \((p\lor q)\)

• \((p\wedge q)\)

• \(\neg q\)

Predicates

\(p\): ___________ ate cereal for breakfast.

We may want to apply the statement to many students, in which case we define a Predicate.

• \(P(x)\): \(x\) ate cereal for breakfast.

• \(x\) can be instantiated to be a particular student, or an arbitrary student.

• \(P(\underline{\hspace{2em}} )\) is a proposition.

Logical Equivalence

Logical Equivalence

Ex: Is it true that \((p \lor q) \equiv (q\lor p)\) ?

Discussion points:

• \(\equiv\) means logically equivalent

• The answer had better be _________!!!

• How can we justify our instinct?

1. Show same truth table
2. Chains of equivalence

Same as saying “write a proof”

Logical Equivalence example

Boolean Masks

Select all the cereals with at least 4 units of protein and no more than 6 units of sugars.

note that by doing this filtering, we are defining a predicate instantiated by each row whose truth value is evaluated.

Challenge: In pandas, test De Morgan with missing data: create a row with protein = NaN. Show that (~p) & (~q) can differ from ~(p | q) under three-valued logic; propose a fix (.fillna(False) or careful NA handling).

Logical Equivalence

“Select all the cereals with at least 4 units of protein and no more than 6 units of sugars.”

\(p\): a cereal has less than 4 units of protein

\(q\): a cereal has more than 6 units of sugars

We suspect that \(\neg p\wedge \neg q \equiv \neg( p\lor q)\):

\(p\)	\(q\)	\(\neg p\wedge \neg q\)
F	F
F	T
T	F
T	T

\(p\)	\(q\)	\(\neg( p\lor q)\)
F	F
F	T
T	F
T	T

half the class complete the TT on the left, the other half on the right, then we all read our responses aloud!

Logical Equivalences

We have discussed Logical Equivalence (LE) and explored an example. The table illustrates LE that are so important, they have names!

Observations:

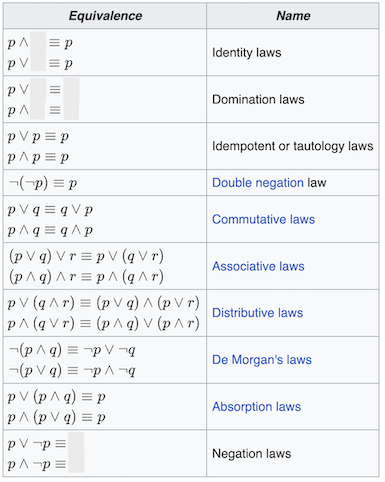
Logical Equivalence Practice

All graded learning activities in the course will use a tool called PrairieLearn.

Navigate to Activity 1 and complete question 2. Each of you will receive a different version of the problem. Work together in pairs to solve each person’s version.

https://us.prairielearn.com/pl/course_instance/186238/assessment/2562335

Implication

Implication

Connect operator \(\rightarrow\) to a logically equivalent expression using only and, or, and not.

\(p\)	\(q\)	\(p\rightarrow q\)	\(\underline{\hspace{3em}}\)
F	F	T
F	T	T
T	F	F
T	T	T

• Is this operator commutative?

• Note: \(p \rightarrow q \equiv\) _______.

• \(p \rightarrow q\) Corresponds to “if \(p\) then \(q\)”

• Gives us mechanism for reasoning!

q and not p is false. so it’s NOT (q^-p) == ??? (apply demorgan)

PL exercises on Logical equivalence involving implication?

More on implication and logical equivalence in tutorial questions

Special Logical Equivalences

Suppose \(p\equiv\) T . Then \(p\) is a Tautology.

Suppose \(p\equiv\) F . Then \(p\) is a Contradiction.

Logical Equivalence Practice

link to PL question

Words and Ideas

Grammar

Predicate

Boolean Mask

Logical Equivalence

Implication