Appendix A: Lecture 13

Appendix A: Lecture 13#

import os
import sys

sys.path.append(os.path.join(os.path.abspath(".."), "code"))

import IPython
import matplotlib.pyplot as plt
import mglearn
import numpy as np
import pandas as pd
from IPython.display import HTML, display
from plotting_functions import *
from sklearn.dummy import DummyClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score, cross_validate, train_test_split
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.preprocessing import StandardScaler

from sklearn.metrics import ConfusionMatrixDisplay  # Recommended method in sklearn 1.0


%matplotlib inline
pd.set_option("display.max_colwidth", 200)

from IPython.display import Image
pd.set_option("display.max_colwidth", 200)
DATA_DIR = "../data/"

(Optional) Search and score#

  • Define a scoring function \(f(S)\) that measures the quality of the set of features \(S\).

  • Now search for the set of features \(S\) with the best score.

General idea of search and score methods#

  • Example: Suppose you have three features: \(A, B, C\)

    • Compute score for \(S = \{\}\)

    • Compute score for \(S = \{A\}\)

    • Compute score for \(S= \{B\}\)

    • Compute score for \(S = \{C\}\)

    • Compute score for \(S = \{A,B\}\)

    • Compute score for \(S = \{A,C\}\)

    • Compute score for \(S = \{B,C\}\)

    • Compute score for \(S = \{A,B,C\}\)

  • Return \(S\) with the best score.

  • How many distinct combinations we have to try out?

(Optional) Forward or backward selection#

  • Also called wrapper methods

  • Shrink or grow feature set by removing or adding one feature at a time

  • Makes the decision based on whether adding/removing the feature improves the CV score or not

# from sklearn.feature_selection import SequentialFeatureSelector

# pipe_forward = make_pipeline(
#     StandardScaler(),
#     SequentialFeatureSelector(LogisticRegression(max_iter=1000), 
#                               direction="forward", 
#                               n_features_to_select='auto', 
#                               tol=None),
#     RandomForestClassifier(n_estimators=100, random_state=42),
# )
# pd.DataFrame(
#     cross_validate(pipe_forward, X_train, y_train, return_train_score=True)
# ).mean()

# pipe_forward = make_pipeline(
#     StandardScaler(),
#     SequentialFeatureSelector(
#         LogisticRegression(max_iter=1000), 
#                            direction="backward", 
#                            n_features_to_select=15),
#     RandomForestClassifier(n_estimators=100, random_state=42),
# )
# pd.DataFrame(
#     cross_validate(pipe_forward, X_train, y_train, return_train_score=True)
# ).mean()

Warnings about feature selection#

  • A feature’s relevance is only defined in the context of other features.

    • Adding/removing features can make features relevant/irrelevant.

  • If features can be predicted from other features, you cannot know which one to pick.

  • Relevance for features does not have a causal relationship.

  • Don’t be overconfident.

    • The methods we have seen probably do not discover the ground truth and how the world really works.

    • They simply tell you which features help in predicting \(y_i\) for the data you have.





(Optional) Problems with feature selection#

  • The term ‘relevance’ is not clearly defined.

  • What all things can go wrong with feature selection?

  • Attribution: From CPSC 340.

Example: Is “Relevance” clearly defined?#

  • Consider a supervised classification task of predicting whether someone has particular genetic variation (SNP)

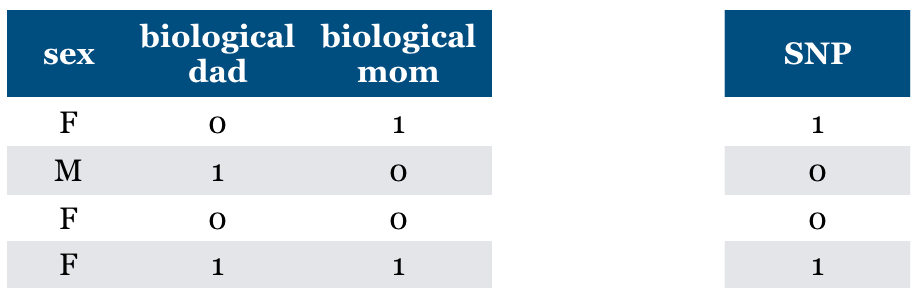
  • True model: You almost have the same value as your biological mom.

Is “Relevance” clearly defined?#

  • True model: You almost have the same value for SNP as your biological mom.

    • (SNP = biological mom) with very high probability

    • (SNP != biological mom) with very low probability

Is “Relevance” clearly defined?#

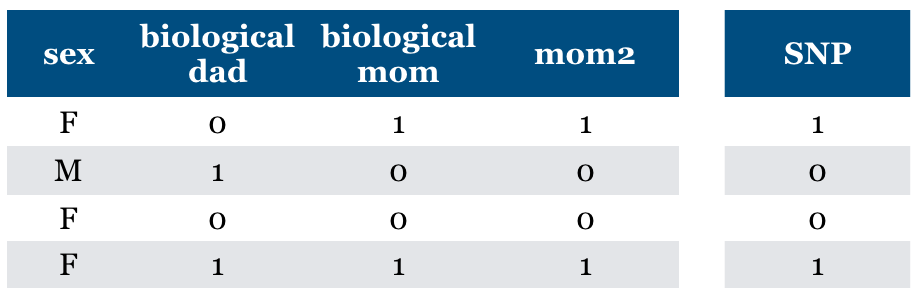
  • What if “mom” feature is repeated?

  • Should we pick both? Should we pick one of them because it predicts the other?

  • Dependence, collinearity for linear models

    • If a feature can be predicted from the other, don’t know which one to pick.

Is “Relevance” clearly defined?#

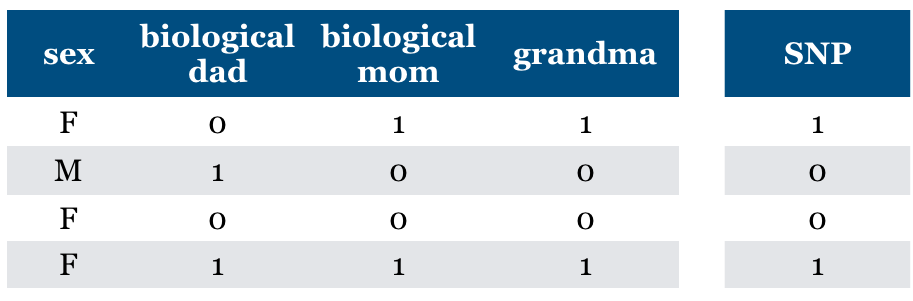
  • What if we add (maternal) “grandma” feature?

  • Is it relevant?

    • We can predict SNP accurately using this feature

  • Conditional independence

    • But grandma is irrelevant given biological mom feature

    • Relevant features may become irrelevant given other features

Is “Relevance” clearly defined?#

  • What if we do not know biological mom feature and we just have grandma feature

  • It becomes relevant now.

    • Without mom feature this is the best we can do.

  • General problem (“taco Tuesday” problem)

    • Features can become relevant due to missing information

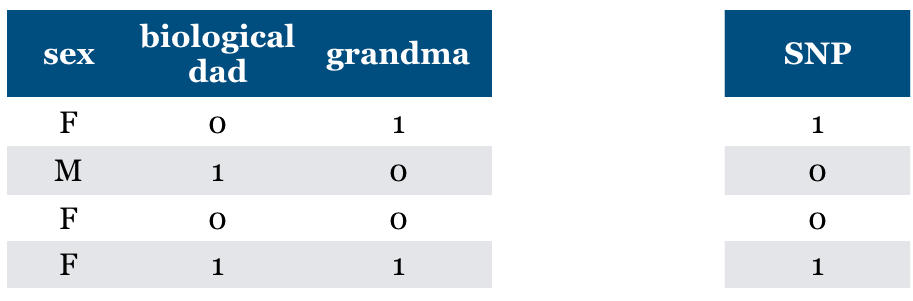
Is “Relevance” clearly defined?#

  • Are there any relevant features now?

  • They may have some common maternal ancestor.

  • What if mom likes dad because they share SNP?

  • General problem (Confounding)

    • Hidden features can make irrelevant features relevant.

Is “Relevance” clearly defined?#

  • Now what if we have “sibling” feature?

  • The feature is relevant in predicting SNP but not the cause of SNP.

  • General problem (non causality)

    • the relevant feature may not be causal

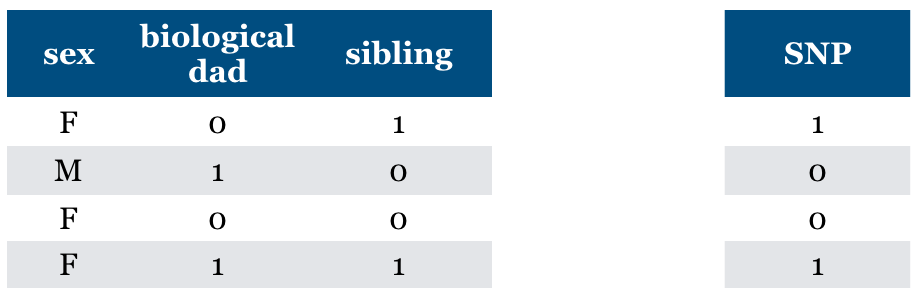
Is “Relevance” clearly defined?#

  • What if you are given “baby” feature?

  • Now the sex feature becomes relevant.

    • “baby” feature is relevant when sex == F

  • General problem (context specific relevance)

    • adding a feature can make an irrelevant feature relevant

Contents