Programming, problem solving, and algorithms

CPSC 203, 2025 W1

November 25, 2025

Announcements

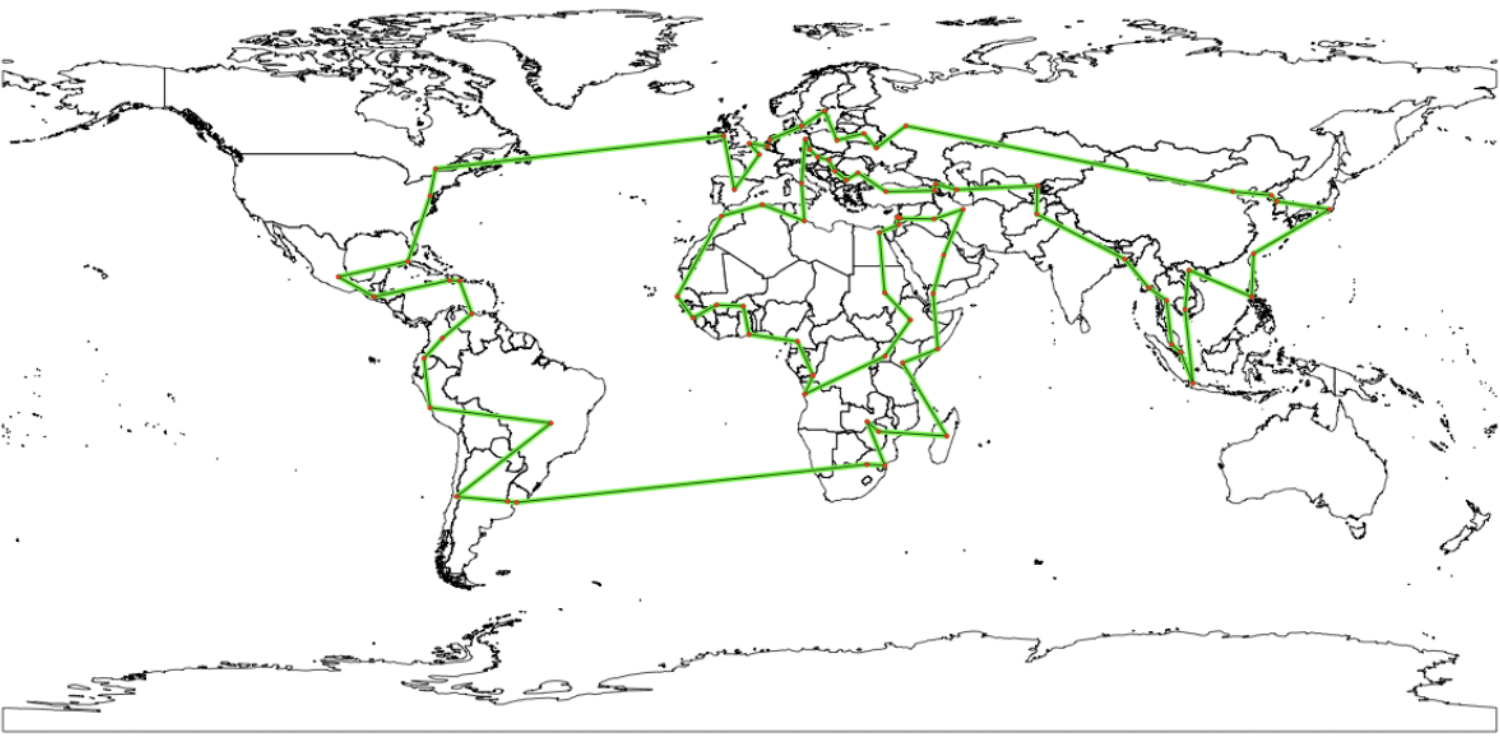
Travelling Salesperson Problem

TSP vs SSSP

SSSP: “many one-way routes from home (tree)” vs TSP: “one big round trip through everyone (loop)”

TSP vs SSSP

Aspect	SSSP (Single-Source Shortest Paths)	TSP (Travelling Salesperson)
Goal	Shortest route from one start to each vertex	One cheapest tour visiting all vertices and returning
Shape	Tree of paths from the source	Cycle through all vertices
Must visit all?	No – each path can skip most vertices	Yes – must visit every vertex exactly once
Overlap	Paths often share edges	Tour is one sequence; no repeated visits
Difficulty	Fast algorithms (e.g., Dijkstra)	NP-hard; exact solution is hard for large graphs

Demo Blog

https://medium.com/data-science/around-the-world-in-90-414-kilometers-ce84c03b8552

Plan for Code

Steps to assemble our solution:

 

1. ________________________________________

2. ________________________________________

3. ________________________________________

4. ________________________________________

5. ________________________________________

1. assemble the graph and errands
2. create pairwise distances
3. create all possible permutations of paths
4. find minimum route and assemble turn-by-turn for that route
5. visualize on map

A Technical Detail

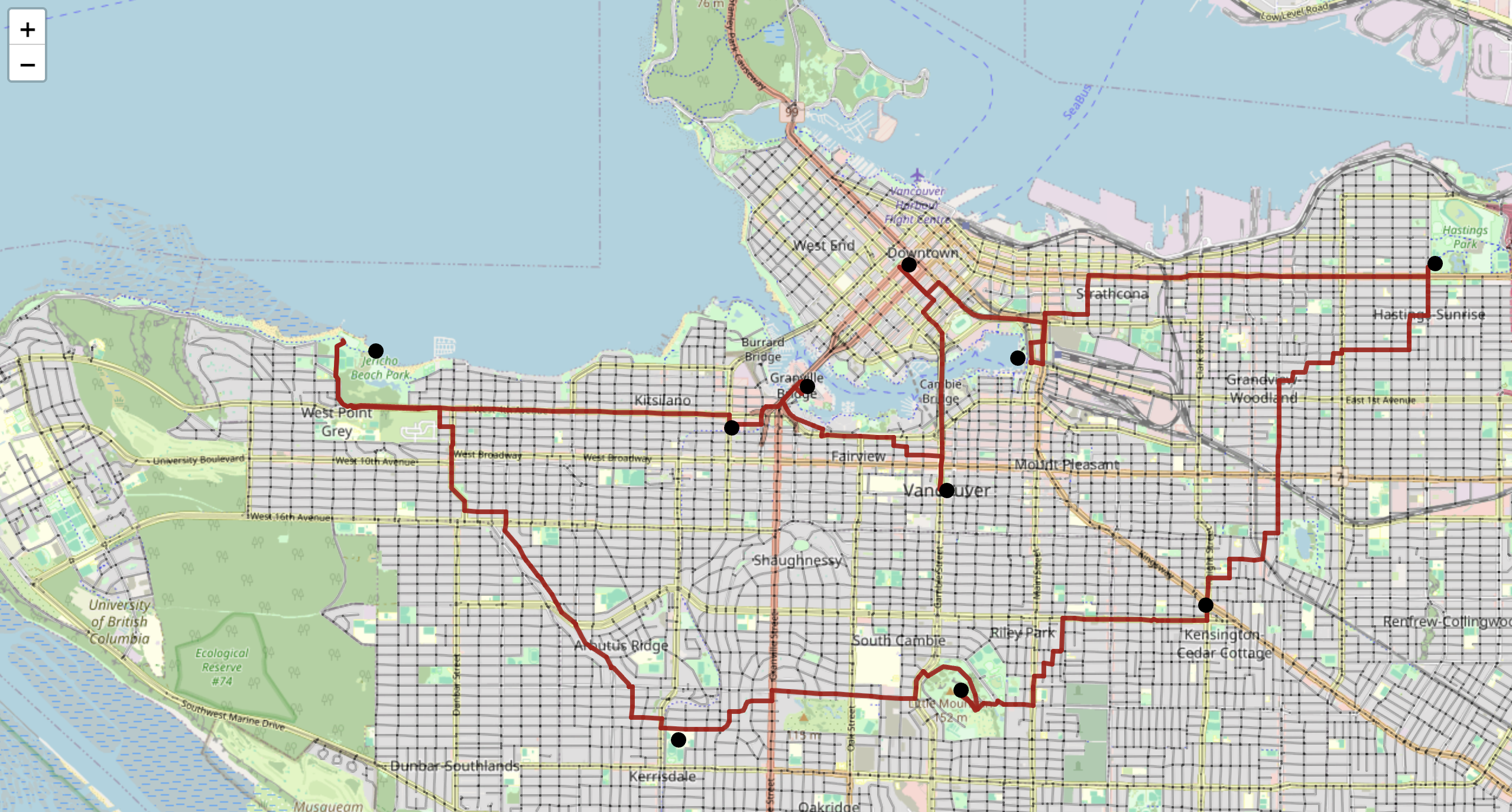
Demo

PrairieLearn Activity

What Does lambda Do?

dferrands['latlong'] = dferrands.apply(
                lambda row: ox.geocode(row['errand']),
                axis=1
              )

Goal: Create a new column (latlong) and fill it with coordinates for each errand in the dataframe.

How it works:

• df.apply(..., axis=1): Run a function once for each row.

• lambda row: ox.geocode(row['errand']): A tiny inline function. Read it as: “Given a row, look up the place name in row['errand'],geocode it, and return the (lat, lon).”

• The returned value becomes the entry in the new latlong column.

Why lambda? We only need this function once, so we write it right where it’s used.

Tour Distance

We assemble each candidate solution as an arrangement of all of the errands:

Ex: A D B E F C

How do we find the total distance if we do the errands in the suggested order?

Why This Matters

There are lots of applications:

• 📦 UPS/FedEx/Amazon Delivery Millions saved by reducing even 1km per driver per day.
• 🍔 UberEats/DoorDash/Skip Multi-stop pickup/delivery with time windows.
• 🧬 DNA Sequencing & Genome Assembly Ordering fragments relies on TSP-like reconstruction.
• 🚌 School Bus Routing Minimize buses, fuel, and time while meeting constraints.
• 🧪 Medical Lab Sample Pipelines Robotic arms schedule efficient multi-station workflows.
• ❄️ Snowplow & Garbage Truck Routing Efficiently cover every street in a city.
• 🏭 Factory Robots & CNC Machines Optimizing tool paths reduces waste, heat, and wear.
• ✈️ Airline Crew Scheduling Complex daily routing: crews must return to base, meet rest rules.
• 🌍 City Infrastructure Planning Utility inspections, meter reading, streetlight repair routes.
• 🚑 Ambulance & Emergency Routing Minimize response times; life-critical optimization.