Programming, problem solving, and algorithms

CPSC 203, 2025 W1

November 18, 2025

Announcements

Maps

Geographic Applications

The data we use for computation is separate from the visualization.

Open Street Maps

 

An open-source alternative to Google Maps’ data.

 

https://www.openstreetmap.org/

 

OSM provides an Application Programmer’s Interface (API) that allows our program to request data, which is returned in a reasonable format.

import osmnx as ox

place_names = ['UBC','Vancouver','Stanley Park']
ox.geocode_to_gdf(place_names)

From Maps to Graphs

OpenStreetMap gives us raw geographic data (intersections, roads, tags)

osmnx converts this into a graph:

  • nodes = intersections (lat/long)

  • edges = roads with attributes (length, max speed, etc.)

We apply graph algorithms to find routes, or substructures.

Finally: visualize results using Matplotlib or Folium

Map Applications

Three Parts

  1. Assembling the data - OSM, local data stores, statsCan, etc. This is mostly the art of assembling geodataframes.

  2. Computing on the data - library osmnx simplifies graph algorithms and computation, but also supports other spatial computation.

  3. Visualizing the data - matplotlib for static maps, folium for interactive maps. Other alternatives available.

Introductory Demo

PrairieLearn Activity

What We’ll See in the Demos

  • Convert map data to graph

  • Identify amenities (Starbucks)

  • Compute shortest route between two landmarks

  • Visualize everything interactively

Single Source Shortest Path

Given a start vertex (source) \(s\), find the path of least total cost from \(s\) to every vertex in the graph.

Single Source Shortest Path

  • Input: directed graph \(G\) with non-negative edge weights, and a start vertex \(s\).
  • Output: A subgraph \(G’\) consisting of the shortest (minimum total cost) paths from \(s\) to every other vertex in the graph.

Dijkstra’s Algorithm (1959)

SSSP Algorithm

Given a source vertex \(s\), we wish to find the shortest path from \(s\) to every other vertex in the graph.

  1. Initialize structure:

    • d:
    • p:

  2. Repeat these steps:

    • Label a new (unlabelled) vertex \(v\), whose shortest distance has been found
    • Update \(v\)’s neighbors with improved distance and predecessor

SSSP Algorithm

  1. Initialize structure:

    • For all v,
      • d[v] = INF,
      • p[v] = null

  2. Initialize source: d[s] = 0

  3. Repeat these steps n times:

  • Find minimum d[] unlabelled vertex: v
  • Label vertex v
  • For all unlabelled neighbors w of v,
    • If (_________________ < d[w])
      • d[w] = ______________
      • p[w] = v

Three Observations:

  • When a node becomes labeled, its shortest distance is final. It will never improve again.

  • d[] values only decrease, never increase.

  • The predecessors p[] form a shortest-path tree.

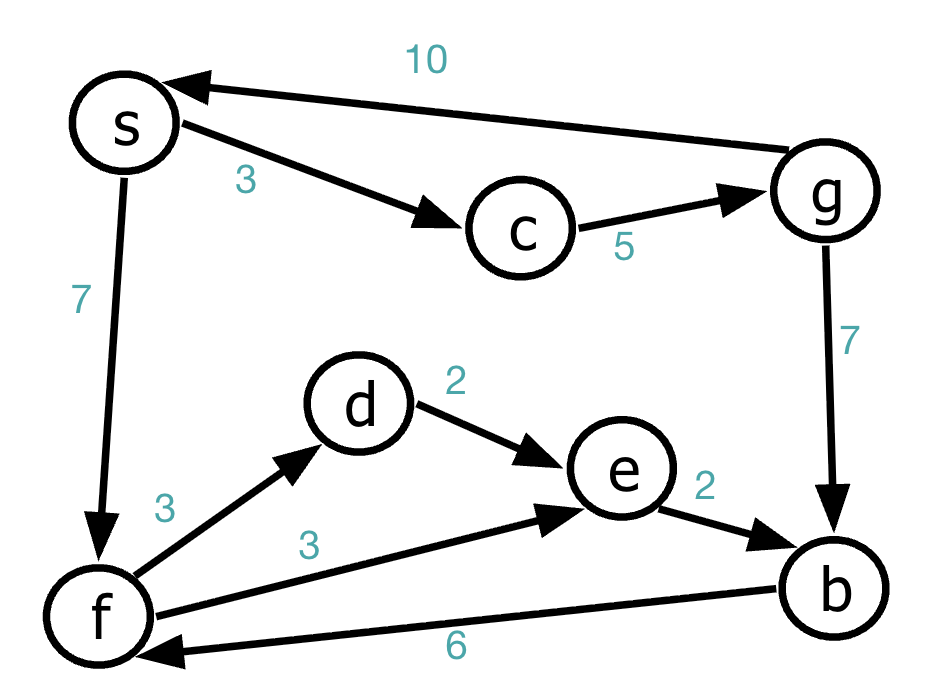
Your Turn

Execute Dijkstra’s algorithm on this graph:

Dijkstra’s Algorithm

  1. Initialize structure:

    • For all v,
      • d[v] = INF,
      • p[v] = null

  2. Initialize source: d[s] = 0

  3. Repeat these steps n times:

  • Find minimum d[] unlabelled vertex: v
  • Label vertex v
  • For all unlabelled neighbors w of v,
    • If (_________________ < d[w])
      • d[w] = ______________
      • p[w] = v
  • How is the algorithm similar to BFS/DFS?

____________________________________ ____________________________________ ____________________________________

  • How is the algorithm different from BFS/DFS?

____________________________________ ____________________________________ ____________________________________

Final Demo

PrairieLearn Activity

What We’ll See in the Demos

  • Convert map data to graph

  • Identify amenities (Starbucks)

  • Compute shortest route between two landmarks

  • Visualize everything interactively

What have we Learned?

Algorithm Data Structure Costs? Shortest? Frontier
DFS Stack ignored no dive deep
BFS Queue all equal yes explore in layers
Dijkstra Priority Queue any non-neg yes explore by shortest known distance

Resources