Programming, problem solving, and algorithms

CPSC 203, 2025 W1

November 20, 2025

Announcements

Single Source Shortest Path, Fin

Geographic Applications

The data we use for computation is separate from the visualization.

Dijkstra’s Algorithm

  1. Initialize structure:

    • For all v,
      • d[v] = INF,
      • p[v] = null

  2. Initialize source: d[s] = 0

  3. Repeat these steps n times:

  • Find minimum d[] unlabelled vertex: v
  • Label vertex v
  • For all unlabelled neighbors w of v,
    • If (_________________ < d[w])
      • d[w] = ______________
      • p[w] = v
  • How is the algorithm similar to BFS/DFS?

____________________________________ ____________________________________ ____________________________________

  • How is the algorithm different from BFS/DFS?

____________________________________ ____________________________________ ____________________________________

Final Demo

PrairieLearn Activity

What We’ll See in the Demos

  • Convert map data to graph

  • Identify amenities (Starbucks)

  • Compute shortest route between two landmarks

  • Visualize everything interactively

What have we Learned?

Algorithm Data Structure Costs? Shortest? Frontier
DFS Stack ignored no dive deep
BFS Queue all equal yes explore in layers
Dijkstra Priority Queue any non-neg yes explore by shortest known distance

Resources

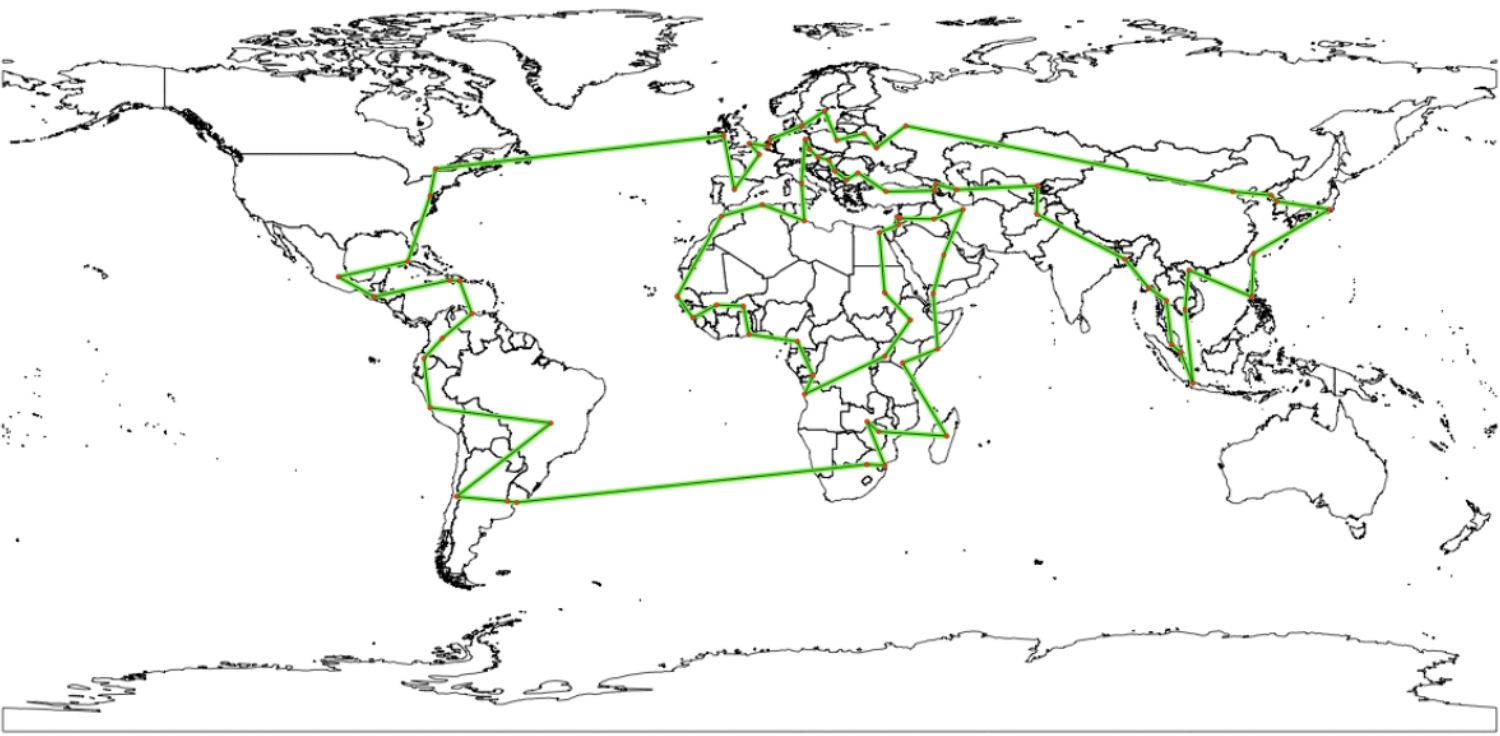
Travelling Salesperson Problem (TSP)

Maps: Running Errands

Determine the least cost route through a set of given locations, returning to the start.

Travelling Salesperson Problem (TSP)

“Given a list of cities, and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?”

  • Classic problem on graphs

  • First known mention was in 1930

  • ________________________________________

How many routes?

Suppose you have 6 locations. How many different candidate solutions are there? Generalize to k locations?

________________________

 

________________________

 

________________________

 

________________________

 

________________________

Demo Blog

https://medium.com/data-science/around-the-world-in-90-414-kilometers-ce84c03b8552

Plan for Code

Steps to assemble our solution:

 

  1. ________________________________________

  2. ________________________________________

  3. ________________________________________

  4. ________________________________________

  5. ________________________________________

A Technical Detail

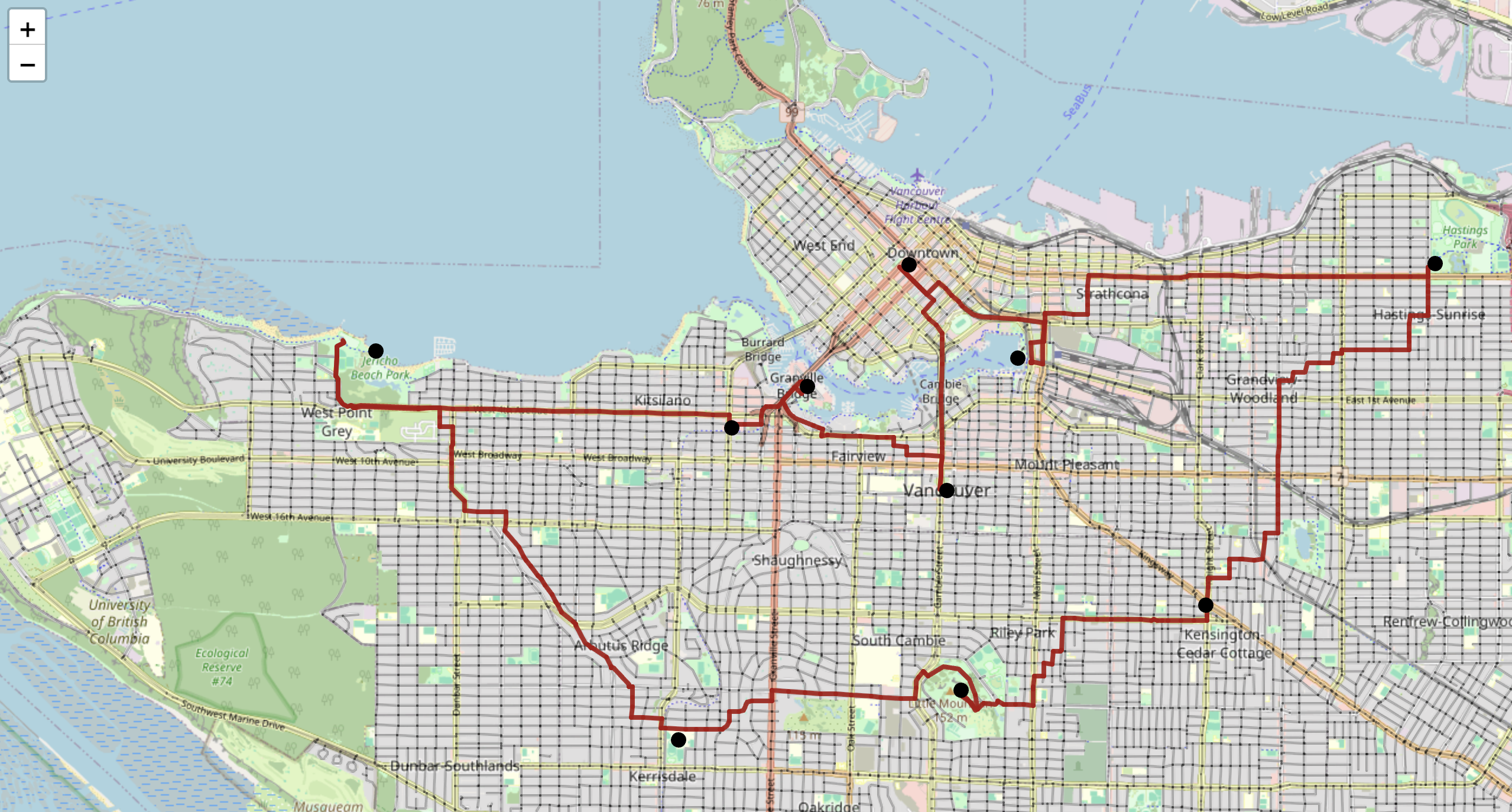
Demo

PrairieLearn Activity

What Does lambda Do?

dferrands['latlong'] = dferrands.apply(
                lambda row: ox.geocode(row['errand']),
                axis=1
              )

Goal: Create a new column (latlong) and fill it with coordinates for each errand in the dataframe.

How it works:

  • df.apply(..., axis=1): Run a function once for each row.

  • lambda row: ox.geocode(row['errand']): A tiny inline function. Read it as: “Given a row, look up the place name in row['errand'],geocode it, and return the (lat, lon).”

  • The returned value becomes the entry in the new latlong column.

Why lambda? We only need this function once, so we write it right where it’s used.

Tour Distance

We assemble each candidate solution as an arrangement of all of the errands:

Ex: A D B E F C

How do we find the total distance if we do the errands in the suggested order?

Why This Matters

There are lots of applications:

  • 📦 UPS/FedEx/Amazon Delivery Millions saved by reducing even 1km per driver per day.
  • 🍔 UberEats/DoorDash/Skip Multi-stop pickup/delivery with time windows.
  • 🧬 DNA Sequencing & Genome Assembly Ordering fragments relies on TSP-like reconstruction.
  • 🚌 School Bus Routing Minimize buses, fuel, and time while meeting constraints.
  • 🧪 Medical Lab Sample Pipelines Robotic arms schedule efficient multi-station workflows.
  • ❄️ Snowplow & Garbage Truck Routing Efficiently cover every street in a city.
  • 🏭 Factory Robots & CNC Machines Optimizing tool paths reduces waste, heat, and wear.
  • ✈️ Airline Crew Scheduling Complex daily routing: crews must return to base, meet rest rules.
  • 🌍 City Infrastructure Planning Utility inspections, meter reading, streetlight repair routes.
  • 🚑 Ambulance & Emergency Routing Minimize response times; life-critical optimization.