Programming, problem solving, and algorithms
CPSC 203, 2025 W1
November 13, 2025
Announcements
Sudoku
Rush Hour

Graph \(G = (V, E)\)
- \(V\):
- \(E\):
Path:
Representing Sudoku
- A representation of a system is a model of the system that is useful in analysis.
- A state space is a collection of all possible configurations of a physical system.
- Each configuration is described using its representation, and is called a state.
How would you represent the game of Sudoku?
State Space Graphs
Define a graph where every vertex is ________________________, and edge (u,v) means ________________________.
How many neighbors does this vertex have?

TicTacToe State Space Graph
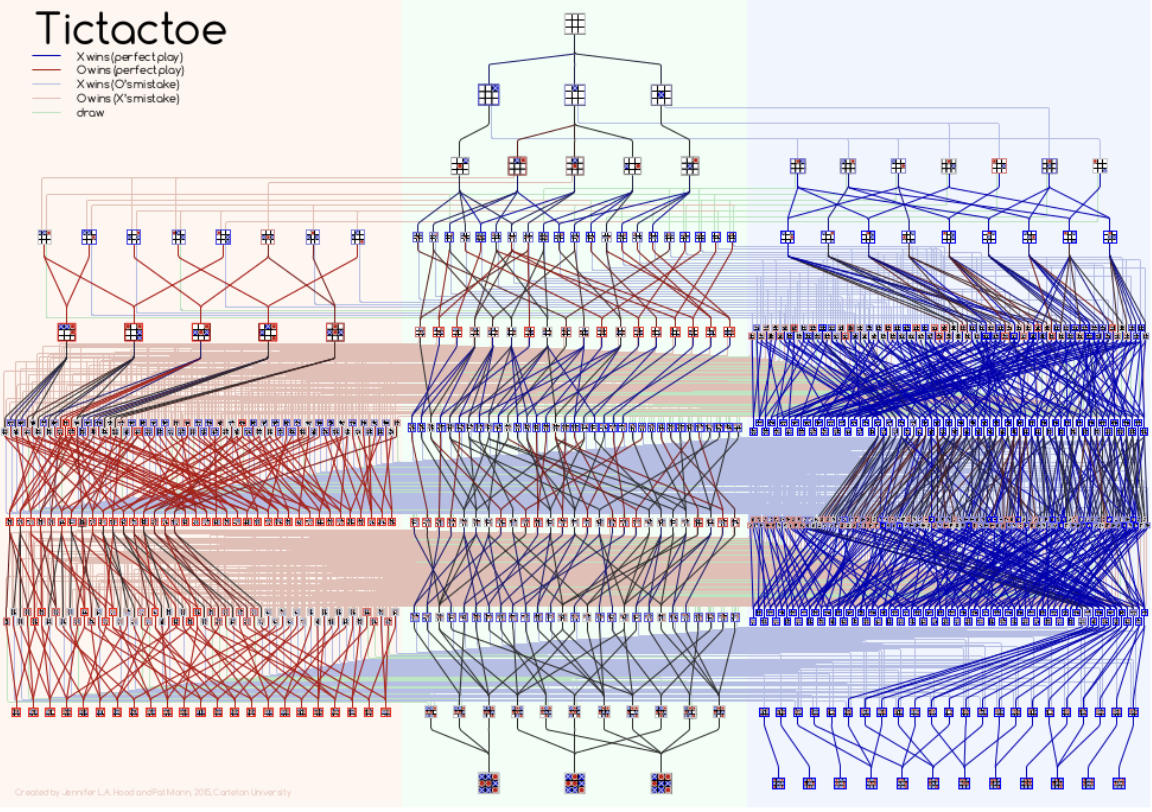
Searching State Space Graphs
Depth First Search


Stacks
Programmatic manifestation of a ________________.
Stack functions:
- Insert:
push(item) - Remove:
pop()\(\rightarrow\)item
Deque functions:
- Insert:
append(item) - Remove:
pop()\(\rightarrow\)item

Flood Fill
- enqueue the center
- while the queue is not empty:
- v = dequeue
- for each valid neighbor w of v:
- process w
- enqueue w
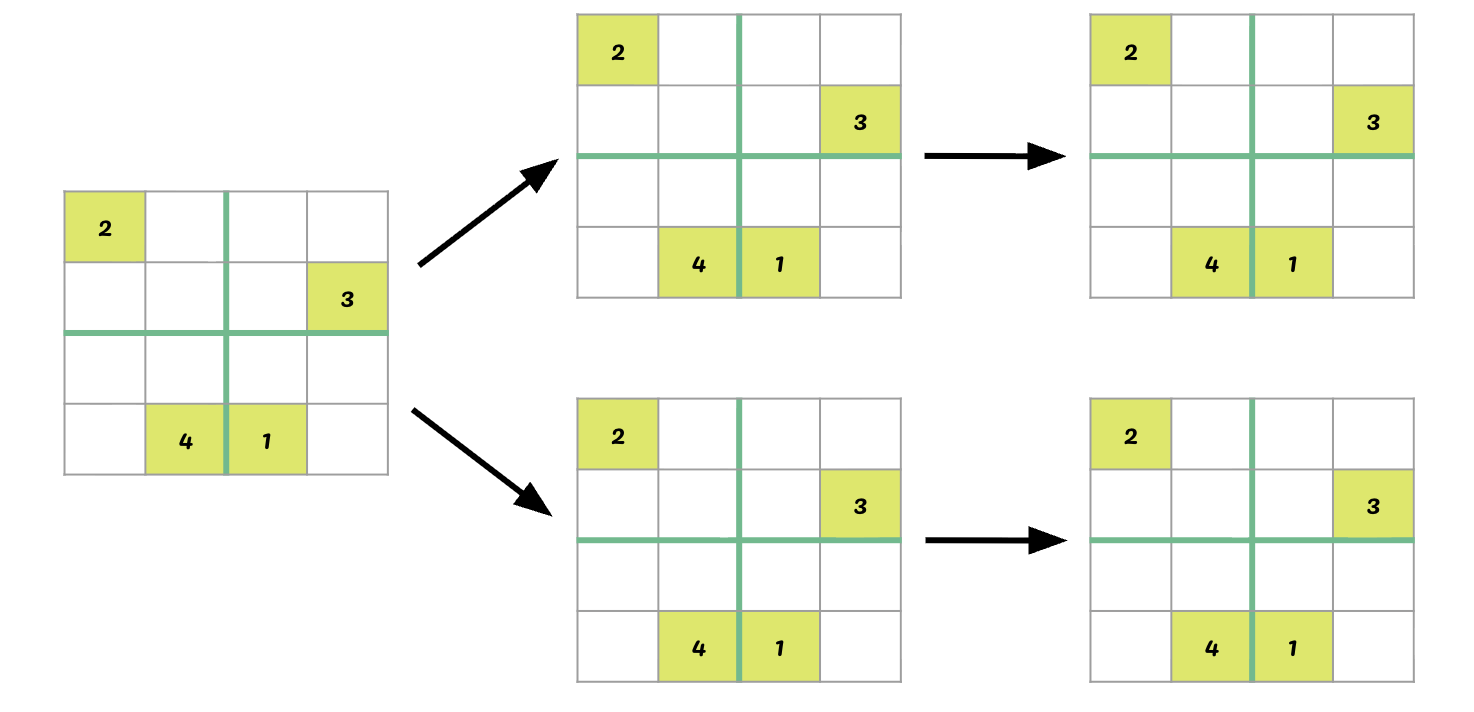
Depth First Search
- process start vertex
push(start_vertex)- while the
stackis not empty:- v =
pop() - for each valid neighbor
wofv:- process w
push(w)
- v =
Algorithm Planning
Overall strategy:
- Move forward through the states (board configurations) until you can’t go any farther.
- If the board is complete, you win!
- If the board is not complete, then back up and try a new state in the most recent cell possible.
Searching State Space Graphs

Moving toward implementation
Need to be able to check whether a candidate entry is valid.
Suppose we have a variable grid, representing the board, and we want to place a value called num, in position (x,y).
Need to check uniqueness in:
- row
- column
- block

Which conditional checks a row?
Which conditional checks a column?
How shall we check a block?
Block Validity
Python tidbit: to query a region in a 2d numpy matrix, just define the bounds on the region and use in.
In the small example below, 2 in grid[0:2,0:2] returns True.

New puzzle: given a location (x,y) how do we define its region?
Defining Regions
Given location \((x,y)\), determine the region in which it lives.
a region
s:tcontains \(x\) if \(s\leq x< t\)for a \(4\times 4\) grid, the block size is 2


Generalize
Find the region for point \((x,y)\) in a \(r^2\times r^2\) grid.
Hint: In python, x//r is the integer part of “x divided by r”.
Another Puzzle
The locations in sudoku are specified by \((x,y)\). As we advance our solution, we can loop over the ranges of \(x\) (\(W\)) and \(y\) (\(H\)), but it would be easier if we could just iterate over the values 0 up to \(W\times H\).
Write a function postup that takes an integer position p as input, and returns an (x,y) position. You may assume that the height and width of the grid is stored in a variable called states.

Demo
A Closing Thought
Could we be smarter?
Another Closing Thought
Is our solution to Sudoku “tractable”? (how fast does the state space grow, as we increase the board size?)
- 3: 9x9
- 4: 16x16
- 5: 25x25
- 6: 36x36
Sudoku is known to be “NP-Complete”.