Programming, problem solving, and algorithms
CPSC 203, 2025 W1
October 30, 2025
Announcements
Graphs
Rush Hour

Graph \(G = (V, E)\)
- \(V\):
- \(E\):
Path:
State Machine
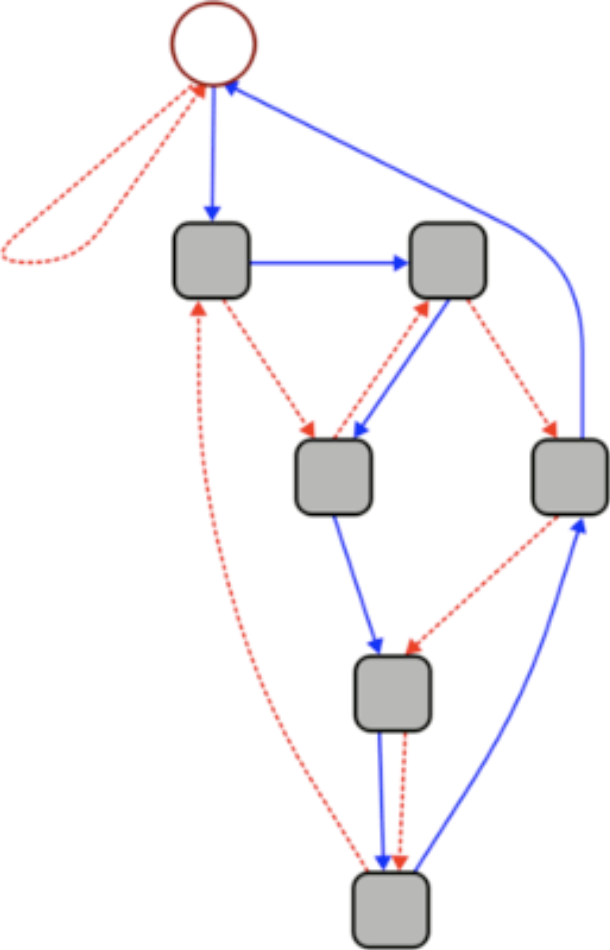
This graph can be used to quickly calculate whether a given number is divisible by 7.
Start at the circle node at the top. For each digit \(d\) in the given number, follow \(d\) blue (solid) edges in succession. As you move from one digit to the next, follow 1 red (dashed) edge. If you end up back at the circle node, your number is divisible by 7.
3703
The Stanford Bunny

Graph \(G = (V, E)\)
- \(V\):
- \(E\):
Planar Graph:
Graph Explorations
A graph \(G\) is defined by a set of vertices \(V\), and a set of edges \(E\).
Algorithm running time is typically described using the number of vertices, but execution usually depends on the number of edges, so we must understand the relationship between them.
How Many Edges?
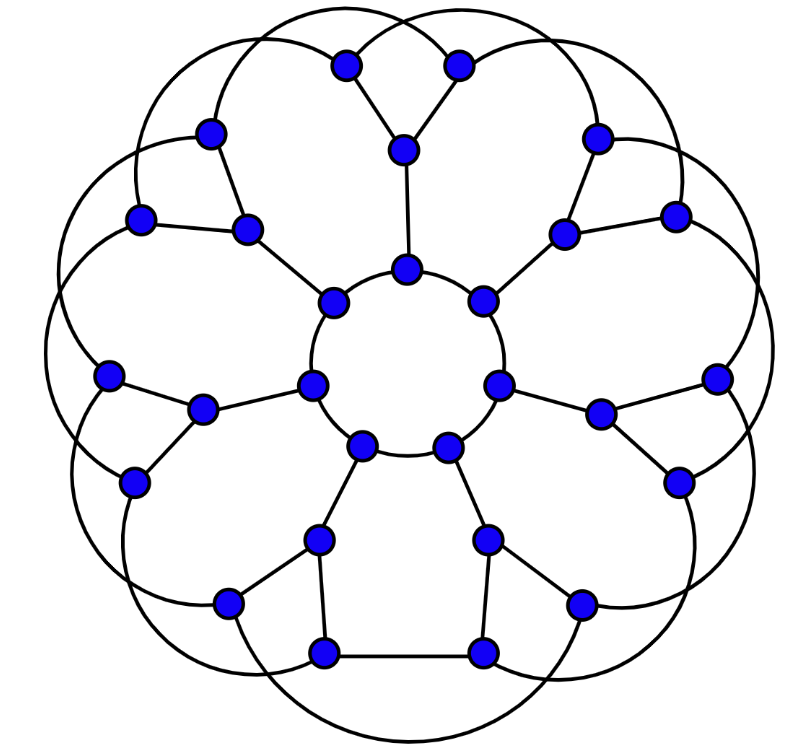
Suppose I tell you a connected graph has 100 vertices. What do we know about the number of edges?
At least __________ edges because the graph is connected.
At most _________ edges which occurs when the graph is complete.
Handshaking
Suppose I tell you a graph has 28 vertices, each with degree 3. How many edges does it have?
The following are equivalent:
- The number of neighbors of a vertex.
- The number of incident edges of a vertex.
- The degree of a vertex.
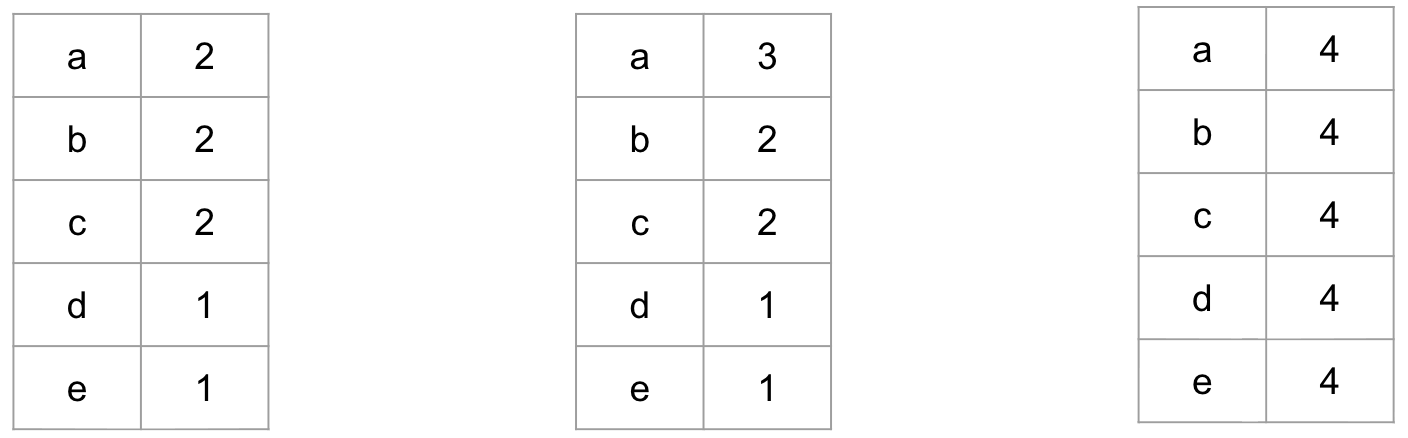
Degree Games
Suppose I drop my graph and it shatters into pieces. If I tell you the degree of each of the vertices, can you reconstruct the graph?
An algorithm for finding a graph, given a degree sequence, is described in the practice problems.
Pencil Puzzles
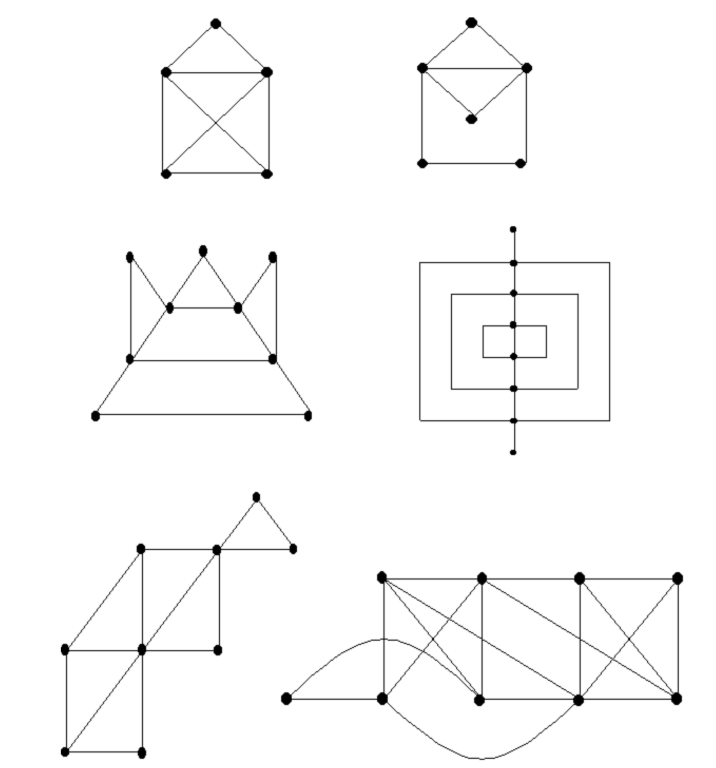
Trace each graph without lifting your pencil and without revisiting an edge.
Can all graphs be traced?
What characterizes those that cannot?