Programming, problem solving, and algorithms

CPSC 203, 2025 W1

October 23, 2025

Announcements

Voronoi Diagrams

Pointillism

A Sunday on La Grande Jatte

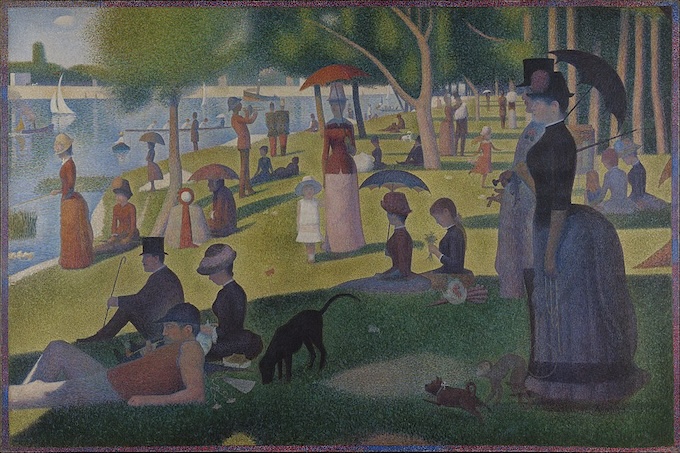
Demo

PrairieLearn Activity

Analysis

How much work is done? Let \(n\) denote the size of the image, \(n = width \cdot height\)

1. Read image:

2. Choose centers:

3. Build new image:

 

4. Write out new image:

Can we do better?

 

Running time of original algorithm: ________

What would be better? ________

 

• Orchestrate a fill from each center, growing out at the same rate.

• Each pixel is processed exactly once, not once per center as before.

• This means we can have lots of centers!

Data Structure: Queue

To implement the fill we use a datastructure called a QUEUE.

Queue:

  enqueue(k) – places data k onto the structure, at the “end”
  dequeue() – removes and returns the “first” element from the structure

Flood Fill

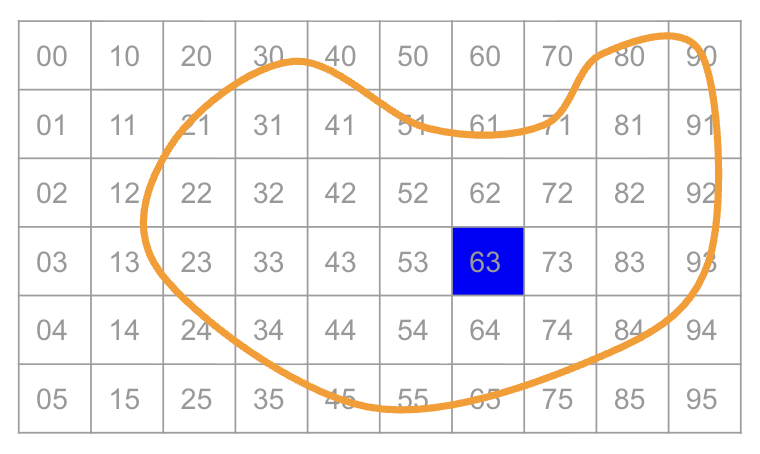
• enqueue the center
• while the queue is not empty:
  • v = dequeue
  • for each valid neighbor w of v:
    • process w
    • enqueue w

Voronoi Art

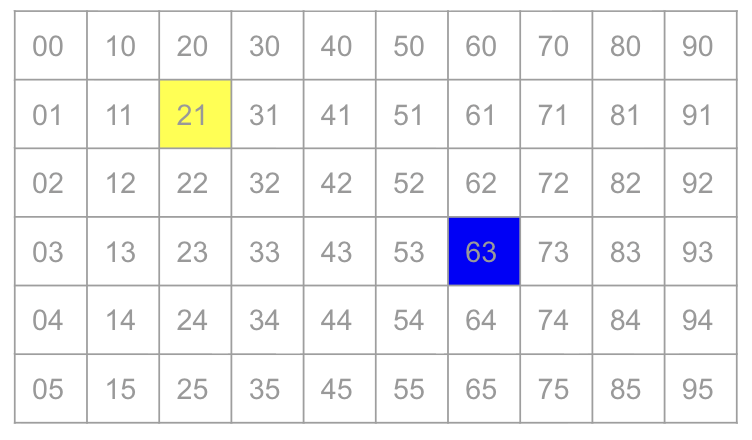
• enqueue the centers
• while the queue is not empty:
  • v = dequeue
  • for each valid neighbor w of v:
    • process w
    • enqueue w

Designing a Solution

 

1. What should we put on the queue?

 

2. We’ll use a Python deque as our queue. What deque functions will we use?

 

3. Do deques have a way to check for empty?

 

4. What are the “neighbors” of pixel (x,y)?

 

5. What would be an invalid neighbor?

Demo

PrairieLearn Activity

Analysis

How much work is done? Let \(n\) denote the size of the image, \(n = width \cdot height\)

1. Read image:

2. Choose centers:

3. Build new image:

 

4. Write out new image:

Graphs: A new model for representing images

• A Graph is a collection of vertices, and edges between them. They’re used as a general model for many problems.

• In our images every ____________ is a vertex, and every ____________ is an edge.

Our fast algorithm for Voronoi Art mirrors a classic algorithm on graphs called Breadth First Search.

Breadth First Search

 

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level. (–Wikipedia)

 

Simplified description: