Programming, problem solving, and algorithms

CPSC 203, 2025 W1

October 16, 2025

Announcements

Voronoi Diagrams

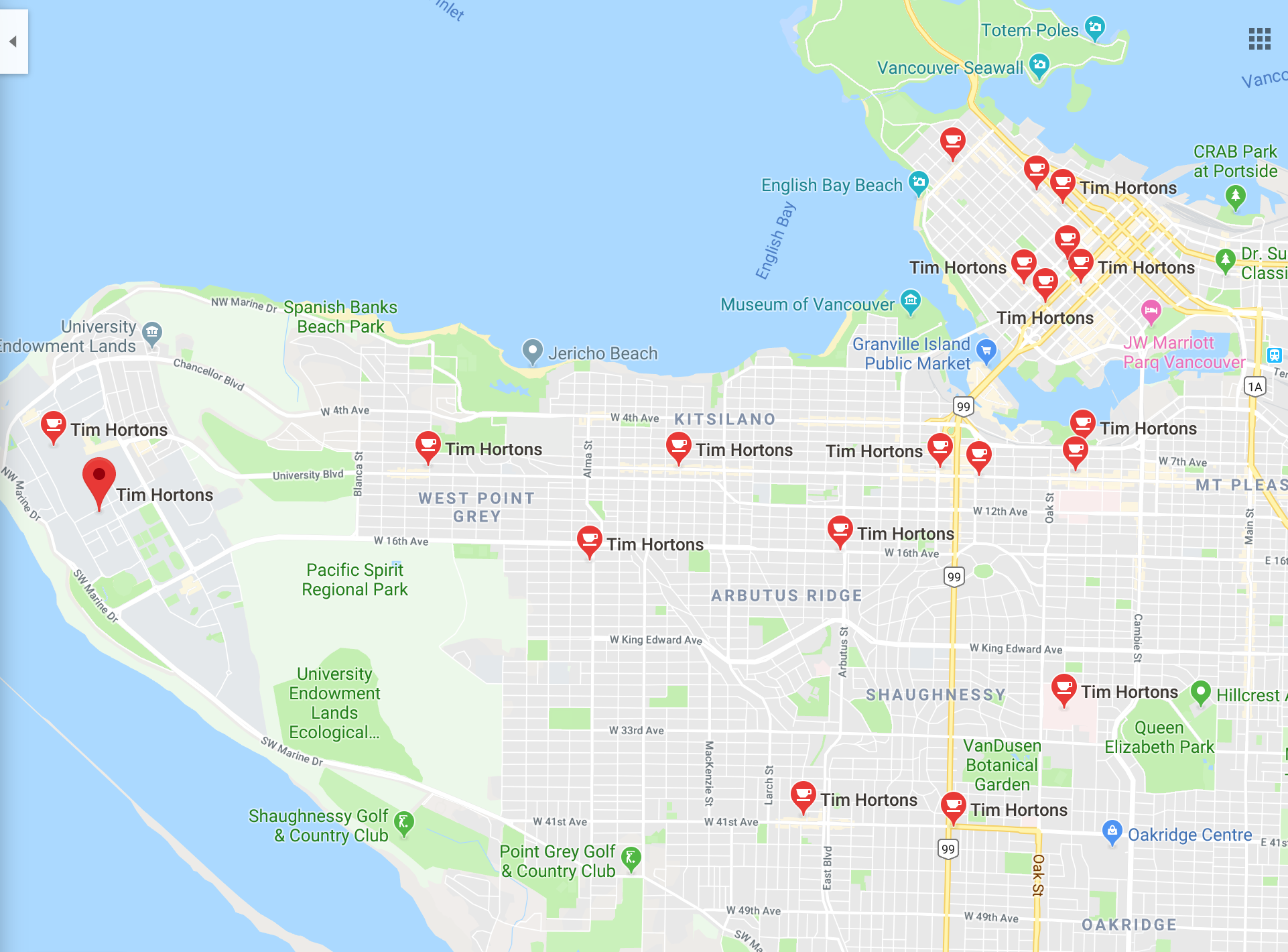
Everyone needs a Tim Horton

Every address in Vancouver has a nearest TH.

Partition Vancouver into regions so that points are in the same region if they have the same nearest TH.

A map of Vaoncouver on the western part of the Burrard Peninsula with pins marking Tim Hortons locations.

Voronoi diagrams

Given a (finite) set of “centres” \(c_{1}, c_{2}, \ldots, c_{k}\), a Voronoi region, \(R_{j}\) consists of the set of points nearer to centre \(c_{j}\), than to any other centre.

Together, the \(R_{j}\) regions compose the Voronoi diagram of a plane.

A map of Vaoncouver on the western part of the Burrard Peninsula with pins marking Tim Hortons locations.

Aerial view of trees illustrating how the tree tops resemble and can be modeled as Voronoi diagram.

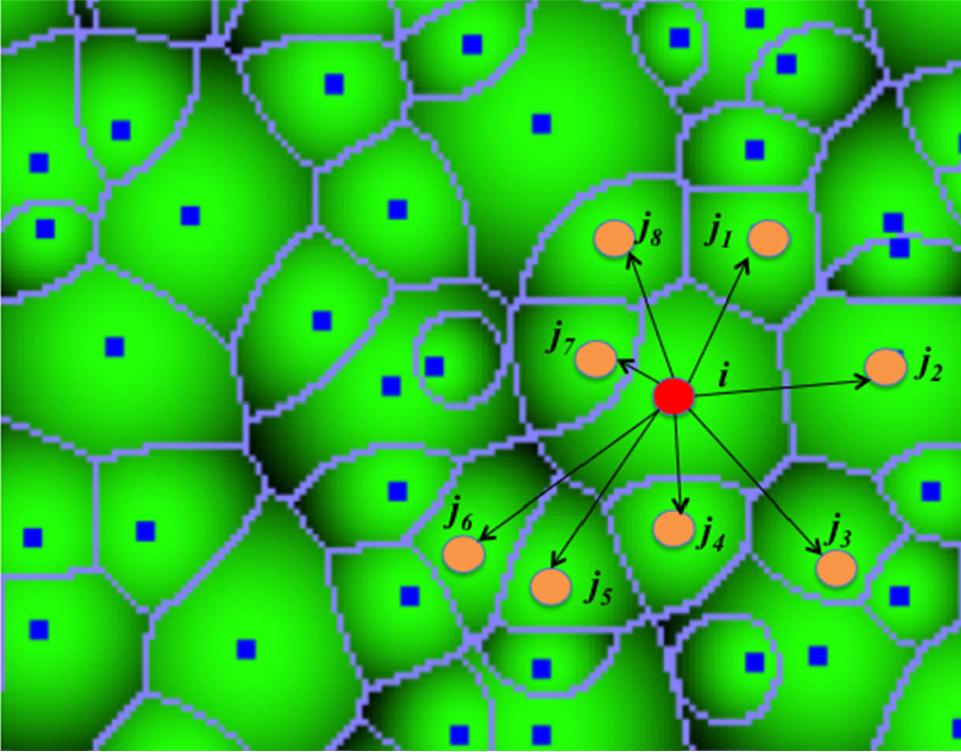
Voronoi diagram of trees showing their centres and regions.

From Abellanas et al. (2016)

More Examples

https://www.khanacademy.org/partner-content/pixar/pattern/dino/v/patterns2_new

A computer generated dinosaur leg with scales.

Yet More Examples

  • Robotics – Path planning in the presence of obstacles

  • Zoology – Model and analyze the territories of animals

  • Astronomy – Identify clusters of stars and clusters of galaxies

  • Biology, Ecology, Forestry – Model and analyze plant competition

  • Cartography – Piece together satellite photographs into large “mosaic” maps

  • Geography – Analyzing patterns of urban settlements

  • Marketing – Model market of US metropolitan areas;

  • Metallurgy – Modelling “grain growth” in metal films

  • Meteorology – Estimate regional rainfall averages, given data at discrete rain gauges

  • Physiology – Analysis of capillary distribution in cross-sections of muscle tissue to compute oxygen transport (“Capillary domains”)

  • Anthropology and Archeology – Identify regions under the influence of different neolithic clans, chiefdoms, ceremonial centers, or hill forts.

  • Crystallography and Chemistry – Study chemical properties of metallic sodium); Modelling alloy structures as sphere packings (“Domain of an atom”)

  • Geology – Estimation of ore reserves in a deposit using info obtained from bore holes; modelling crack patterns in basalt due to contraction on cooling

Computing Voronoi Diagrams

Choice of algorithm depends on the domain of the data.

 

If real valued domain (like Cartesian Coords) then we use geometry, exploiting the fact that the Voronoi edges are perpendicular bisectors of the edge between 2 centers.

 

Our computation will always be on planar regions represented by images.

 

Data for the problem:

Data for the solution:

Distance Between Pixels

 

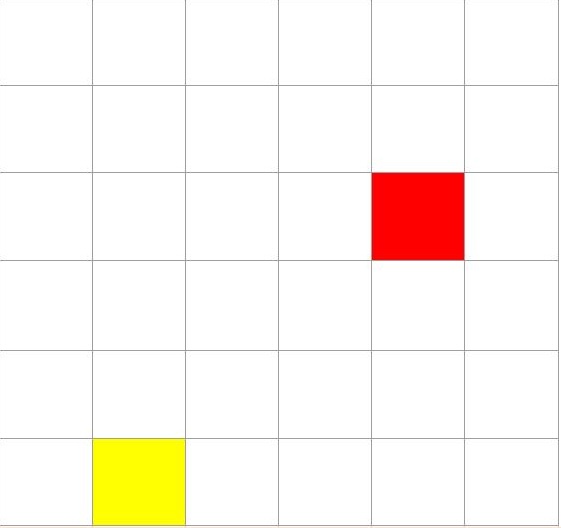
Find the distance between 2 pixel locations:

A 6x6 grid with 2 colored cells.

Distance Between Pixels

Given a point and two centers, determine which is the nearest center…

:A 6x6 grid with 2 colored cells.

A 6x6 grid with 2 colored cells.

Design an Algorithm

A large grid with 3 colored centers.

References

Abellanas, Begoña, Manuel Abellanas, Arne Pommerening, Dolores Lodares, and Simón Cuadros. 2016. “A Forest Simulation Approach Using Weighted Voronoi Diagrams. An Application to Mediterranean Fir Abies Pinsapo Boiss Stands.” Forest Systems 25 (2): e062–62. https://doi.org/10.5424/fs/2016252-08021.